Temperature dependence of theoretical strength of materials with high melting temperature.
A method is proposed for determining the temperature dependence of the theoretical strength of refractory substances on the basis of an analysis of the function of the change in the potential energy of the body from the relative elongation, calculated from the experimental data on the modulus of elasticity, the coefficient of thermal expansion, density, temperature dependence of the heat capacity and melting point.
INORGANIC MATERIALS
VOLUME 25 • N 5 • 1989
offprint (rus))
The advance of mechanical engineering requires the creation of structural materials that retain high strength values at the maximum possible operating temperatures. Among most high melted refractory compounds and elements, nitride and aluminum oxide, silicon nitride and silicon carbide, boron carbide, partially stabilized zirconium oxide and sialons are most promising for the creation of such materials [1]. It is of interest to compare the values of the theoretical strength of refractory substances at high temperatures in order to identify those that, along with these, could be recommended for in-depth studies on the possibility of obtaining high-temperature structural materials on their basis.
The number of papers [2-6] is devoted to the problems of calculating the theoretical strength of materials on the basis of an analysis of two-particles interaction potential . The problem of determining the temperature dependence of the theoretical strength was considered in [7], where it was shown that the theoretical strength decreases linearly with increasing square of the average amplitude of atomic oscillations in a solid.
In this paper, we propose a method for calculating the temperature dependence of the theoretical tensile strength on the basis of an analysis of the function of the change in the potential energy A U(x) of a material in solid state from the relative elongation x = (l - 1o) / lo, where lo and l are the linear dimensions of the body in equilibrium state and under the action of the external force, respectively.
Let's consider for specificity sake the cylinder made from one mole of substance, with the area of section - S. Its tensile strength corresponds to the maximum stress that arises in the body when it is continuously stretched. The stress at the relative elongation of the body x is related to the function of changing the potential energy as follows:
| σ = (1/(S×l))×(∂ΔU/∂x) | (1) |
Considering that for small relative elongations, l ≈ lo and S×l is equal to the volume of 1 mole Vm = S×l = M / d, where M is the molecular weight and ρ is the density, the tensile strength is:
| σb = (ρ/M)×(∂ΔU/∂x) x=xmax | (2) |
where xmax is the elongation corresponding to the maximum tensile stress.
Let us consider the basic relations connecting the function of the potential energy change ΔU(x), the specific form of which, generally speaking, is unknown to us, with the physical-chemical and mechanical properties known from experiment. We also assume that the dependence of the change in the internal atomic interaction potential on the relative change in the internal atomic distance x = (r - r0) / r0, where r0 and r are the average distances between atoms in a solid body at absolute zero without external pressure and under it, respectively, these coincide to within a coefficient equal to the effective number of bonds in the direction of extension, with the function ΔU(x).
From the general form of the function ΔU(x), we can write:
| ΔU(0) = 0 | (3) |
| (∂ΔU/∂x)x=0 = 0 | (4) |
Relation (4) expresses the fact that greatest energy benefit of the equilibrium state. Proceeding from Hooke's law and relation (1), we write
| (ρ/M)×(∂ΔU/∂x)x→0 = E×x | (5) |
where E is the modulus of elasticity. The function U (x) can be related to the coefficient of thermal linear expansion as follows:
| α = (dy/dT) = (Cp/3)×( (ρ/M)×(∂λT/∂ΔU)(∂y/∂λT) | (6) |
where y = (l0 (T) - l0) / l0, where l0 (T) is the equilibrium length at temperature T, Cp is the specific heat at temperature T, and the value of ∂y/∂λT is determined by the rule for derivative of implicit functions from equation
| ΔU×(λT + y) - ΔU×(- λT + y) = 0 | (7) |
where λT is the average amplitude of the thermal vibrations of the atoms, referred to the distance between atoms.
We also assume, in agreement with [8], that the relative elongation xmax, corresponding to the maximum of the discontinuous voltage and determined from relation
| (∂2ΔU/∂x2)x=x max = 0 | (8) |
corresponds to a change in the potential energy of the body, transferring it with increasing temperature to a different phase state (melting point, sublimation). From here
| ΔU(xmax) = (1/3)× ΔH0(T0) | (9) |
where ΔH0(T0) is the change in enthalpy when the body is heated from absolute zero to the phase transition temperature To. Here and in formula (6), the coefficient 1/3 expresses the fact that thermal energy is distributed to the three degrees of freedom of atoms oscillation. Starting from the mutually independent equations (3) - (9), we can determine coefficients in the function A U(x), given in an explicit form, for example, as the potential of Mie or Morse. Since the values of Xmax are usually sufficiently small (0.1 - 0.3), the function ΔU(x) can be represented as a power series of the type of the Maclaurin series. Restricting ourselves to the terms of the expansion not higher than the fourth, we can write explicitly
| ΔU(x) = a×x2 + b×x3 + c×x4 | (10) |
where the coefficients a, b are determined from relations (5) - (7) and are equal
| a = E×M/2ρ | (11) |
| b = - (α/Cp)×(E2M2 /ρ2) | (12) |
and the coefficient c is found as a result of solving equations (8) and (9), which can be written in an explicit form as follows:
| ΔH0(T0) = 2.5×a×xmax2 +1.5×b×xmax3 | (13) |
| c = - (a- 3×b×xmax)/(6×xmax2)) | (14) |
At high temperatures, as a solid body model, we take a crystal in which the atoms are in extreme average deviations from the equilibrium position at a given temperature, with an equal number of positive and negative deviations. This model is used implicitly in the derivation of the coefficient of thermal expansion. The values of the average atomic deviations of λT+ and λT- in extreme positions of thermal oscillations at a temperature T can be calculated by solving the equation:
| ΔH(x)/3 = a×x2 + b×x3 + c×x4 | (15) |
where ΔH(T) is the change in the enthalpy when the body is heated from absolute zero to T, and the stress arising from the stretching of a σT(x) at temperature T is determined by the formula
| σT(x) = 1/2 ×(ρ/M)×∂/∂x[U(λT+ + x) +U (λT- + x)] | (16) |
where λT+ and λT- are the roots of equation (15).
Suppose that the destruction at temperature T occurs at such a relative elongation x at which the average energy of the atoms with positive deviations from equilibrium becomes equal to the critical OH0 (To / 3. The magnitude of the critical elongation is then calculated as the positive root of equation
| [ΔH0(T0) - ΔH0(T)]/3 = a×xm2 + b×xm3 + c×xm4 | (17) |
and the strength by substituting the value of xm found in equation (16).

|
||
| Temperature dependencies of the theoretical tensile strength for most common ceramics: SiC (1), AlN (2), ZrO2 (3), MgO (4), Al2O3 (5), Si3N4(6), SiO2 (7) | ||
The figure shows the temperature dependencies of the theoretical strength calculated by this method on the basis of reference data [9-14] for the most common ceramics. It should be noted that the total loss of strength occurs up to the melting point, which agrees with the strength test data of real ceramics [9, 10, 13].
The results of a comparison of the theoretical strength shown in the table for various refractory compounds showed that the most common ceramics do not always have the highest theoretical strength and its choice as a basis for the development of high-temperature ceramics is often due to low cost, chemical and thermal stability and technological considerations. At the same time, for critical parts that are operated in a neutral environment at particularly high temperatures, it is necessary to pay attention to such compounds as TaC, NbC, HfC, HfB2, TiC, TiN, TaB2, which retain high values of theoretical strength up to 2500 K.
| Theoretical tensile strengths (σb, 10-10 Pa), calculated by formulas (11) - (17) for the most stable compounds at high temperatures |
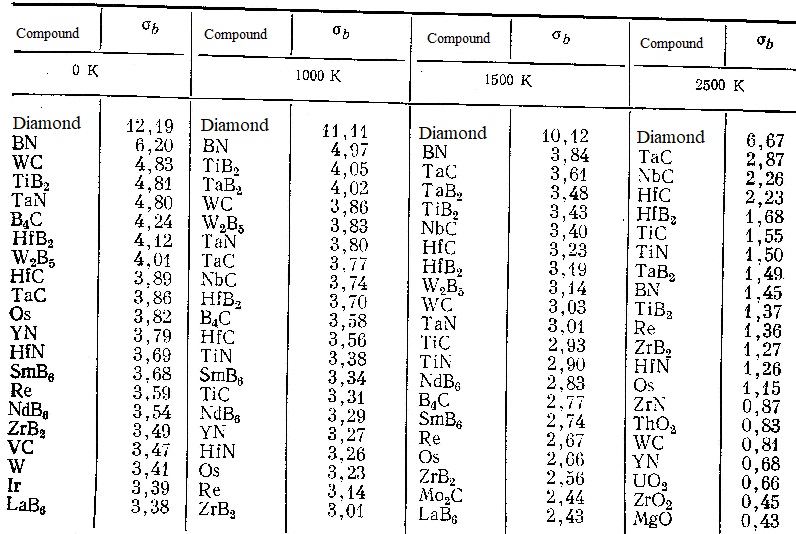
|
Using the proposed method, it is also possible to calculate the temperature dependencies of the elasticity modulus E and the thermal expansion coefficient a, which is important for evaluating the compatibility of various compounds in high-temperature composite materials, as well as the stability of high-temperature coatings.
Conclusions.
A method is proposed for determining the temperature dependence of the theoretical strength of refractory substances on the basis of an analysis of the function of the change in the potential energy of the body from the relative elongation, calculated from the experimental data on the modulus of elasticity, the coefficient of thermal expansion, density, temperature dependence of the heat capacity and melting point.
Bibliography
1. Kulik O. P, Denisenko E. T, Krot O. I. High-temperature structural
ceramics. Preparation and properties: Preprint Ns 2. Kiev: IPM
Academy of Sciences of the Ukrainian SSR, 1985. 10 p.
2. Izotov A.D, Lazarev V.B. The destruction of ceramics at high-speed
loads from the point of view of physical chemistry. J..
Phys.Chemistry. 1986. T. 55. N 1.p. 192-196.
4. Izotov A. D, Lazarev V.B. Theoretical Strength of Ceramic
Materials. Izv. AN USSR. Inorgan. Mater. 1985. Vol. 21. Ns 5. p. 706-711.
5.Kelly A. Strong solids. L. • Oxford Univ. Press., 1966. 263 p.
6.Barteniev GM Strength and mechanism of polymer destruction.
M .: Chemistry, 1984. 279 p.
7. Zwicky F. Die Reifestigkeit von Steinsalz. Phys. unserer Zeit. 1923.
Bd. 24. Ns 6. S. 131-137.
8. Osipov K. A. The relationship between the theoretical strength
and the speed of crack propagation during a crust the destruction
of metals with their thermodynamic parameters melting. Dokl.
AN USSR. 1983. T. 271. N 3. p. 657--660.
9. Properties, production and application of refractory compounds,
Ed. Kosolapova T. Ya. M .: Metallurgy, 1986. 928 p.
10. Physicochemical properties of oxides, Ed. Samsonova G. B.
M .: Metallurgy 1969. 456 c.
11. Frantsevuk I. N., Voronov F.F., Bakuta C. A. Elastic constants
and module of elasticity of metals and non-metals, Kiev: Nauk.
dumka, 1982. 286 p. p.
12. Bojtovych P. F. Refractory compounds. Thermodynamic characteristics. Kiev:.
Science. dumka, 1971. 220 p.
13. Ceramics from highly fireproof oxides. Ed. D.Polibojarinov
D.H., Popilckoro P. Ya. M .: Metallurgy, 1977. 304 p.
14. Babushkin V.I., Matveev G.M., Mchhedlov-Petropyan O. P. Thermodynamic
of silicates ~ Publishing house for literature on construction,
1972. 351 p.
|
Institute of Mechanical Engineering them. A. A. Blagonravov
Academy of Sciences of the USSR, Leningrad Branch |
Received by Journal at 27.04.1987 |
Jul. 26, 2018; 09:07 EST