Import data from outside sorce
After opening empty of data LeoDataAnalysis application the first step is add or insert data series:
Step 1. Select source.
In the Control panel of LeoDataAnalysis do click on the tab: "Data" and then click on the button "Add" as it is shown on the picture:
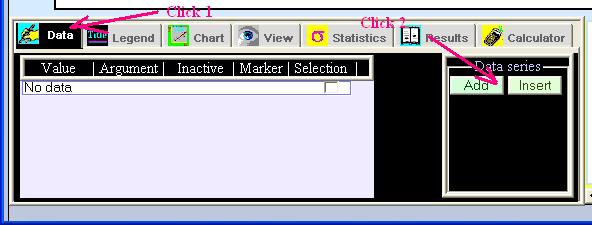
The dialog panel with available options for data import will appear:
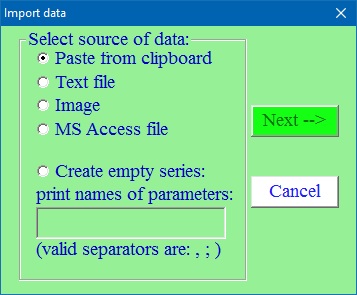
Depending on source of your data check out the corresponding options from:
If you have in mind to type in data into created empty data series (table) you should type in all names of columns. An equivalent number of columns (fields) will be created. Later on you will be able to edit as number of columns as well their names if needed.
If you already have at least one opened data series by this method you can add one more with exact the same number of parameters as in opened one.
After selecting type of outside data source click at button "Next".
Step 2. Import data series.
From clipboard.
If you use external application like a MS Excel for data preparing an import them into LeoDataAnalysis cannot be easier. Just select the region with data, and click "Copy". Then in LeoDataAnalysis choose "paste from clipboard" and click on "Next".
If the first row on selected region contains non-numerical values
LeoDataAnalysis will interpred them as names of parameters. Otherwise
names of parameters will be assigned in style = a0, a1, a2 and so on.
Note: The format of table in clipboard is based on "Tab"
and "Space" separators between cells and "end of string"
used as end of row. Standard sources of such data are spreadsheet
like applications or Tables in MS Access or MS Word. Text file also can be
copy-paste in LeoDataAnalysis.
From text file.
To import data from text file at first do chose the file by browsing your computer that contains data in form one record per line. Two example of legitimate format of such file is presented below:
Example 1 (first line contains names) x y 1.05 3.4 2.3 4.3 5 1.2e1 9 24.0 Example 2: (only numeric fields) 6, 4, 2.0 3, 2.3, 1.0 2e0, 1.2, 7.33 43.1 ,1.e3, 33.6 54, 222, 44.0 77,555, 67.0 99, 777.5, 88.0 104, 1000.e-10, 88.0
The first line can contains a names of columns; if it doesn´t the program
will assign names in the style a0, a1, ... aN where N is number of the column.
The actual dissection of the first line will be present in the appeared dialog
panel for Example 2 like this:
This is actually a wrong situation as soon each field must contain only numerical letters divided by separator letters. By default space and "tab" sign are considered as separators. User can add any number of separators. In presented case the commas are used as separators and as such must be typed in "Separators" edit control as it shown in following picture:
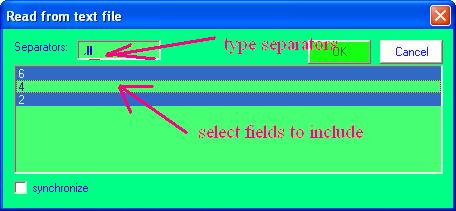
User also can by clicking on the corresponding lines do select fields only these of all existed to be read into LeoDataAnalysis.
Click "OK" to read data.
When a data source is a text file there is special option of automatically renewing data that can be helpful in case of observation of gathering experimental results in real time. To do this:
- Prepare original text file with appropriate number of fields.
- Open the file it as described above. Before clicking on the button "OK" do check "synchronize" control.
-
The dialog
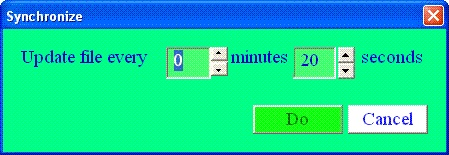will appear. Set period of updating the content of file and press "Do"
button.
- Only one data series can be set synchronized.
- To stop updating any more do perform any updating operation with this data series like for example a deleting. You will be able to perform other evaluations procedures with continuously updating file like editing legend, approximation data and so on.
The example import data from text file spiral.txt will produce following picture when added as a first data series in LeoDataAnalysis:
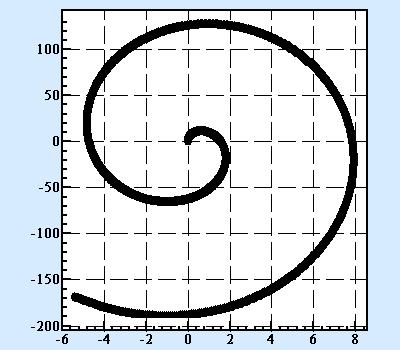
From image.
One of the most unique feature of LeoDataAnalysis is an ability extract and to incorporate data from an image. Scientists often have an impulse when reading article in professional journal to reanalyze data presented in form of chart. To get curves in numerical form is a challenging and let´s say the truth a very dull and time consuming job. LeoDataAnalysis can help to make in fast an accurate.
Chose "Image" and click "Next" in "Import Data" dialog. The window that will give an ability to transfer visual data into numerical form will appear.
Import your picture. There are two options to do this.
1) From any image file in any of most popular formats. Click on the button "From file". Browse and chose the file. All most common formats like bmp, gif, jpg are supported. As an example you can use the image of the picture: temperature dependence of theoretical strength of ceramic materials .
2) Paste image from clipboard. Most useful this option can be in case of internet published articles. Usually internet browsers permit to click on right button of the mouse when cursor is on the image evoking popup menu with element - "copy image". Choose it. Click on button "Paste from image from clipboard" in LeoDataAnalysis and get a picture. Of course any image from clipboard memory will do the job.
Set physical coordinates on the chart: 1) Push down a button "Select chart area" and drag green rectangle expanding it in that way to cover a chart area with your data. Set minimum and maximum values of the rectangle area as it can be read from legend of the axes at the picture.
By clicking by left button on the line or marks user is selecting records
these later on will be imported in LeoDataAnalysis. "Alt +click"
combination will remove the point pointed by cursor. After
reaching satisfying result like shown on picture: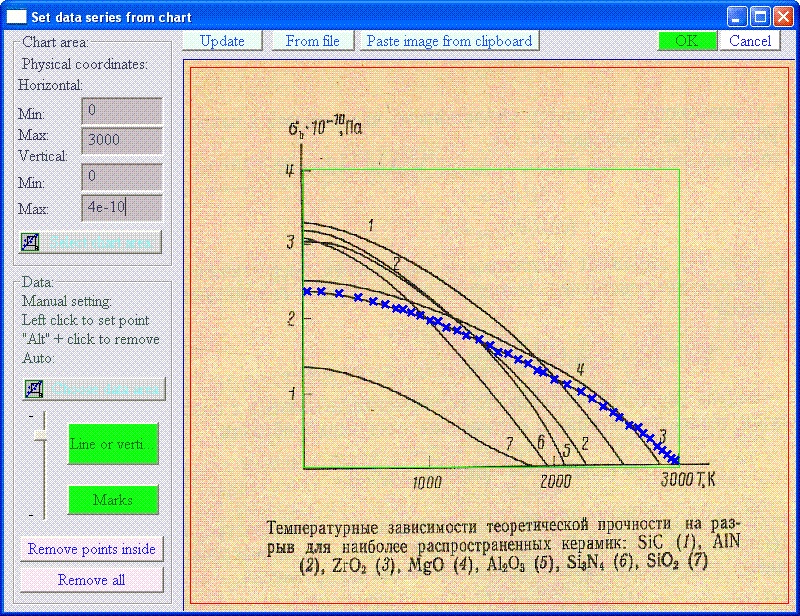 
click on "OK" button. The data series containing two parameters
will be created in LeoDataAnalysis. For presented case the screen of
LeoDataAnalysis will look like this:
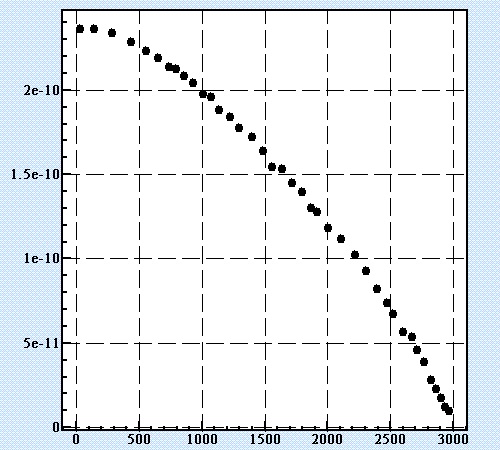
In a case when one curve in the image are contrast enough and
can be isolated, LeoDataAnalysis is able to set marks automatically.
To do this at first press down button "Chose data area" and
drag red rectangle to cover all this area. Press one of two buttons
"Line" or "Marks".
If a result of selection will be not satisfactory click on button
"Remove points inside" and repeat the procedure with other
setting of contrast sensibility.
Create empty series.
LeoDataAnalysis can at once create empty series with number and names of parameters reflected printed in the edit control.
Later actual data have to be print out and all data edited as it is described in data manipulation page. General idea is to press "Show data" button at "Data" tab and manually type data one by one in the grid like control.Pixels color statistics.
LeoDataAnalysis has the ability to read data directly from the image file. To do it go to Menu ⇒ Data ⇒ Read image file ⇒as RGB (or HSV)..
The standard file search dialog will appear. Select any image file and open
it. Depend on what color representation model you will chose
histogram of colors distribution will be displayed. For example
for the picture with basic red, green, blue color areas : 
distribution colors in RGB scheme will be like this: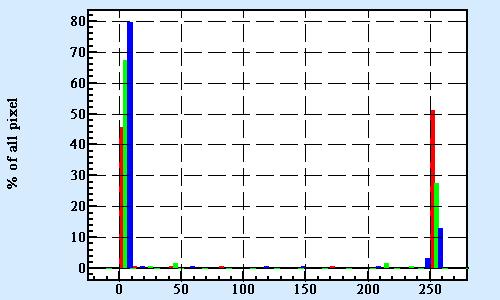 
and for HSV scheme: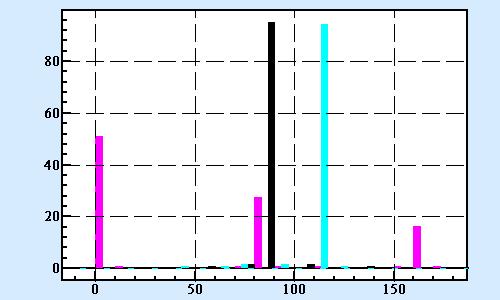 
HSV (Hue - direction from white color - the color itself, Saturation - intensity of color, Value - darkness) scheme of color representation has the advantage of separation colors in image permitting at least to count the number of brushes of palette in the image.
The exact formula of calculating hue is quite complex. One can see that colors of spectra spread from red 0 to red on other side 255 (violet is 200, green 81 and blue 162). Saturation is calculated as an average deviation from value and normalized to interval 0-255. Value in its part is here an average of RGB values.
Note and warning.. The image contains a lot of data. Due to representation of the data in LeoDataAnalysis a million of records that is usual for even average size image file will slow down a time of calculations especially for some of the statistical schemes. Just use common sense and be caution.
From MS Access database file.
LeoDataAnalysis can import data saved in database file. As soon there are numerous formats and variations of SQL syntactic of databases and connection protocols we can only claim compatibility with MS Access. In general we don´t recommend this type of data source if there is any alternative. Usually most database clients have option to save dataset in form of txt file.
Nevertheless if you decide to use your database file as data source for LeoDataAnalysis the routine is following.
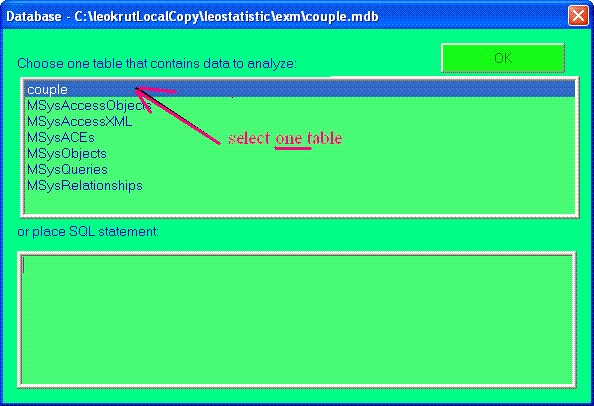In the the dialog do select one table of the database that
contains the data or use advantage of running your own sophisticated
SQL statement to create dataset with special properties that
could sometime perform a fancy job.
Press "OK".
No matter if you select one of the tables or run SQL-statement next "Database" dialog will be displayed with available fields like this.
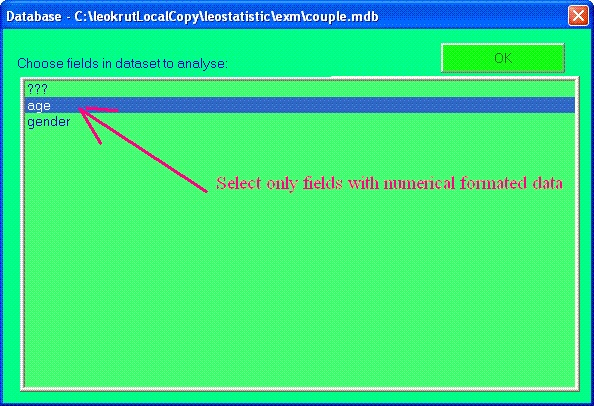
Important to know that only fields in numerical or text format
containing only numerical letters will be read in LeoDataAnalysis. In case of
breaking this rule for any cells all corrupted records will be skipped
during reading. The same is valid for situation if you run SQL-statement.
Click "OK".
As a demonstration of ability of SQL statements to produce meaningful calculation lets solve small statistic-combinatorial problem:
Let presume that we have a data of the age of bachelors males and females in table "couple" in our example couple.mdb database. The task is to find a distribution of all possible age distinctions for different gender couples.
Solution:
1) With the help of master of queries in original database application such as MS Access we will create two query: age_male and age_female by running SQL-statements:
SELECT age INTO age_female FROM couple WHERE gender=”f”
SELECT age INTO age_male FROM couple WHERE gender=”m”
2) Then run LeoDataAnalysis. Go to tab "Data"; click "Add"button; select " couple.mdb" file; type SQL-statement:
SELECT age_male.age-age_female.age as d_age FROM age_male, age_female;
click "OK"; select "d_age" field, click "OK"; go to "View"
tab and click distribution button 
.
The result image will be like this:
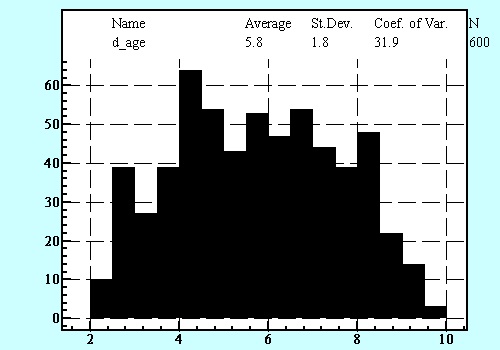
It is worth to note that in the spite that the initial couple table contains only 49 records a result of running shown above SQL statements we will have all possible combinations of age variance in different gender couples - 600 cases at all.