Nucleation energy barrier at crystallization in nonstoichometric composition glass-forming solutions.
The dependence of the energy barrier of nucleation on the composition of the melt is considered. Under sufficiently general assumptions regarding the form of the dependence of the melt concentration in front of the crystal-melt boundary, taking into account the law
of conservation of mass, a unique expression is obtained for the magnitude of the minimum change in the free energy
due to the deviation of the melt composition from the initial one.
Zhurnal Fizicheskoi Khimii
1983, v. 57 N 9, p. 2355-2357. (
rus.)
The dependence of the energy barrier of nucleation on the composition of the melt is considered. Under sufficiently general assumptions regarding the form of the dependence of the melt concentration in front of the crystal-melt boundary, taking into account the law of conservation of mass, a unique expression is obtained for the magnitude of the minimum change in the free energy due to the deviation of the melt composition from the initial one.
For the production technology of glass and glass-ceramic, the dependence of the rate of crystal nucleation on the composition of the melt is of great importance. The general pattern [1] is that melts of stoichiometric composition exhibit maximum propensity to crystallization. The deviation of the composition of the crystallizing melt from stoichiometric causes a sharp decrease in the rate of nucleation. According to the existing concepts [2, 3], the appearance of a crystal nucleus of radius r `is accompanied by a change in the free energy, equal to
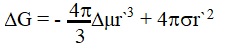
|
(1) |
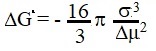
|
(2) |
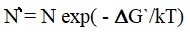
|
(3) |
where N is the number of molecules in the melt. In the case of non-stoichiometric composition in the melt due to the law of conservation of mass, the distribution of the concentration of the crystallizing component ahead of the crystal-melt boundary must be less than in the depth of the melt. In equation (1) it is necessary to add one more term characterizing the change in free energy due to a decrease in the concentration of the melt in front of the boundary of the embryo with the melt from the initial one.
Let us consider the change in the thermodynamic potential due to the concentration term in the case when the range of the composition of the melt is limited by a sphere of radius r', and the dependence of the concentration on the distance to the center of the embryo in front of the melt boundary is described by an arbitrary function c (r) = co - c '(r), where co is the concentration in the original melt and the condition co> c`(r)> 0 is satisfied.
The change in the free energy ahead of the frontal front due to the deviation of the concentration from the initial one is equal to
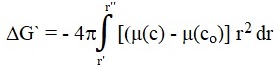
|
where μ(c) is the specific volumetric chemical potential of the melt concentration c (r). Since μ = μo + (RT /v) ln c, where v is the molar volume, we obtain
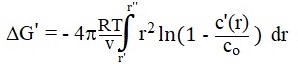
|
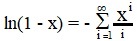 , we have
, we have
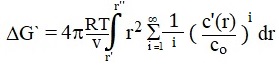
|
(4) |
According to the law of conservation of mass, the function c '(r) must satisfy the normalization condition:
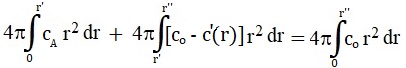
|
(5) |
wherefrom
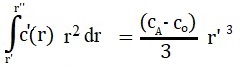
|
Substituting this expression into equation (4), we obtain
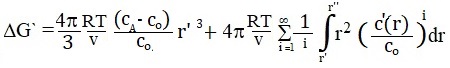
|
(6) |
Since c'(r)> 0, the series in equation (6) must be greater than or equal to zero. Thus, starting from the most general assumptions about the form of the function c '(r), we have the inequality
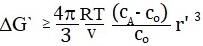
|
Let us consider a more specific form of the function c'(r). Assume that it can be represented in the form c'(r) = a/ rn, where a and n are the coefficients, and n > 3. Then from the normalization condition (5) in the case r' → ∞, we can obtain the value c'(r), from which
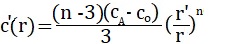
|
Substituting the result obtained for c'(r) into equation (6) as r' → ∞, we have
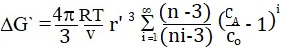
|
If n → 3, then it is easy to verify that ΔG' assumes a minimum value:
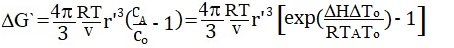
|
(7) |
where ΔH is the melting enthalpy, ΔT = TA - To, where TA and To are the liquidus temperatures of the stoichiometric and initial melts, respectively. The structure of the resulting expression for ΔG' allows us to keep the classical derivation scheme for the barrier equation of nucleation, replacing Δμ by
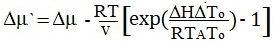
|
(8) |
The dependence of the nucleation rate on the composition of the melt in the case when the influence of the concentration term on the energy barrier is taken into account, as follows from equations (2), (3) and (8), is sharper than in the usual analysis. This effect should be especially pronounced in case of low hypothermia.
Analysis of Eq. (8) for changing the chemical potential during nucleation in a nonstoichiometric melt shows that for small supercoolings there exists a region where N <0, as a result of which the melt becomes stable with respect to small fluctuations and the spontaneous nucleation rate of the crystals is zero. Taking into account that Δμ = ΔHΔT/vTo, and restricting ourselves to the first term in the expansion of the exponential (for most cases it is sufficient), we obtain an expression for the boundary temperature of the region of the relative stability of the melt
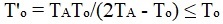
|
The expression for changing the chemical potential Dm 'can then be written in the form close to the standard
| Δμ'= ΔHΔT'/vTo' | (7) |
where ΔT'= To' - T
Literature
1. Gutkina N.G., Mukhin E.Y. In the book. Physico-chemical basis for the production of optical glass. L.: Chemistry, 1976. p. 196-234.
2. Kydyarov B.I. Kinetics of the formation of crystals from the liquid phase. Novosibirsk, Nauka, 1979, 134 p.
3. Christian J. The theory of transformations in metals and alloys. Part 1 M. Mir, 1978, 806 p.
Received by the Editor
10.V.1982
Academy of Sciences of the USSR
Institute of Silicate Chemistry
them. IV. Grebenshchikova,
Leningrad
Apr. 26, 2018; 09:39 EST