The fast algorithm for the numerical simulation of crystal growth.
There are principle methods of algorithm for the numerical simulation of crystal growth these permit dramatically increase its performance by means of pre-calculating all intermediate numbers and presenting them as integers.
The fast algorithm for numerical simulation of crystal growth is the code implementation of the the model of surface of growing crystal described in a page " Physical background of the model for numerical simulation of crystal growth". The model is based on the premise that surface of the growing crystal can be presented as an two dimensional integer matrix L and the scientific background for calculating probabilities of each molecule (that is represented by one element of the matrix L[i,j]) to change positions at the surface of the crystal on the base formulas derived from thermodynamic characteristics of the phase transition and crystallographic parameters of the crystal.
A software implementation of the model for the numerical simulation of the crystal growth have to be as much efficient as possible to permit collection large enough set of numerical experiments for multivariate analysis of results. In our version implemented in LeoMonteCrystal that is written in Visual C++ environment the major efforts was concentrated on the minimization part of operations with float type of variables (these have decimal points in them).
In spite that formulas for probabilities for molecule movement unavoidable demands float point operations like exponent function there is a way to avoid letting them inside loops of simulation itself by following means:
- - parts of surface associated with different directions of cuboid are represents with integer values by scaling whole molecule surface to big enough integer number Sm (to minimize error of rounding) and rounding values of the parts to integers;
- - represent probabilities for molecule to stay in place or to move ahead by integer numbers scaled between 0 and Rmax that is maximum value that generator of random numbers cam produce.
- - calculate two integer two-dimensional matrices with size Sm×Sm there probabilities for molecule to stay in place or move ahead are prevented by integer numbers in the interval 0 and Rmax for all possible combinations of the molecule surrounding on the surface. Note that size of matrices has to be Sm×Sm not just Sm because by our model of quasi-independent behavior of molecule one need to take into account not only current surrounding of the molecule but also its virtual surrounding if the molecule step one move ahead.
- - use integer numbers characterizing molecule surrounding as an indexes in arrays described above for updating probabilities of each molecule to stay or move ahead.
The scheme of fast algorithm for calculation of probabilities of one a molecule movements.
One of most common operation during numerical simulation of crystal growth is defining probabilities for a molecule at given position surface to change its value that it is equivalent movement of crystal surface at this position. Each element of matrix L[i,j] have probabilities to add 1, lose 1 or retain the same value. These probabilities are defined for each time step with two integer matrices with size identical to matrix L: matrix Po[Nb, Nc] contains probabilities for molecule to stay at the same place and matrix P1[Nb, Nc] contains probabilities to move ahead. Integer values of elements Po and P1 represent probability normalized in range of values from 0 to the maximum integer number Rmax that is specific for given generator of random numbers used in software. For implementation of the algorithm in LeoMonteCrystal this value is Rmax = 0xffffffff = 4294967295.
The core procedure of simulation is repeated in infinite loop can be described as following:
At each time step
{
every element of matrix Po[i,j] is compared
with newly generated for each of them separately random number
R and following conditional actions are performed:
{
if R< Po[i,j] then corresponding element of matrix L[i,j] retains previous value;}
otherwise:if R< P1[i,j] (here we know that R is less than Po[i,j] so some action must happen) then L[i,j] is added one(in the specific case when in the algorithm formation hole type defects is considering one specific case must be checked here. If there is well like surrounding the element of matrix L[i,j] when the element is located at the bottom of the hole like formation an addition of the element taken as corking up the well capturing free space inside the well creating hole like defect. In such case depend on depth of the well like construction two or more integer units should be be add and location of the new hole type defect is registered);otherwiseelement matrix L[i,j] will lose one integer units.
(For variant of the algorithm that includes considering formation of hole like defects, the situation if the molecule is corking of the hole beneath it, one or more integer elements are subtracted.)
Update matrices Po and P1.}
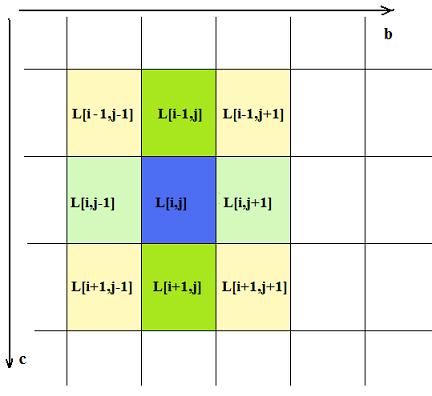
An updating matrices Po and P1 after next in a row time step after calculating movements for each elements must be performed for each element of matrix L that changed value by itself or at least one of its neighbors did. For each changed element there are nine elements whose probabilities have to be recalculated at next step these are including changed element itself and its eight close neighbors. As Fig. 1 shows
|
|
||
| Fig. 1. Element of matrix L surrounded by neighbor elements. |
any given element of matrix L[i,j] has eight neighbor elements of three different sorts, highlighted at Fig 1 with different colors. There are four diagonal neighbors and two distinct pairs of along rows and columns ones. For each of these there cases there is simple conditional algorithm to calculate part of surface of molecule that is in direct contact with crystal body scr. The Table 1 provides rules for values of part of surface δij associated with any neighbor element these should be summed to calculate scr.
| Table 1 | |||
| Lnb - L[i,j] | Lnb = {L[i-1,j], L[i+1,j]} | Lnb = {L[i,j-1], L[i,j+1]} | Lnb = {L[i-1,j-1], L[i+1,j-1], L[i-1,j+1], L[i+1,j+1]} |
| <= -2 | 0 | 0 | 0 |
| -1 | Sac | Sab | Sabc |
| 0 | Sb+Sac | Sc+Sab | Sbc+Sabc |
| <=1 | Sb+2*Sac | Sc+2*Sab | Sbc +2*Sabc |
In the Table 1 value Lnb represents one of the direct neighbors of the updated element L[i,j] of matrix L. First column shows possible difference between tested element and one of his neighbors: Ln - L[i,j]. Corresponding cells of the Table 1 give values δij depend on type of relative position of the neighbor and difference in their values.
An algorithm uses the simple conditional formula to calculate part of molecule on surface in direct contact with crystal as shown in following equation:
| scr = Sa + Σ δij( Ln - L[i,j] ) | (1) |
where δij( Ln - L[i,j] ) - is part of molecule surface to add depend on difference in values with examined molecule and its near neighbor as provided in Table 1. Note that for variant with hole like defects are taken into consideration the formula 1 for molecule that is corking hole is modified by excluding Sa term.
In the chapter " Physical background of the model for numerical simulation of crystal growth" that describes physical background of the method values of surface parts in different crystallographic directions: Sa, Sb, Sc, Sab, Sac, Scb, Sabc are presented as integer numbers scaled (normalized) to also integer number Sm that gives whole surface of the molecule:
| Sm = 2*(Sa + Sb +Sc) +4*(Sab + Sac + Scb) + 8 *Sabc | (2) |
For calculation probability of moving molecule on the crystal by the model of quasi-independent behavior of molecules we need two numbers for characterization of surrounding if each molecules on surface part of molecule surface in contact with other near neighbor molecules belonged to crystal phase: first in current position and second at the virtual position that molecule could occupy if it is mounted (added) above current position. Because as we stated above parts of surface belonged to faces, edges and vertices are integers all possible combinations of an molecule surroundings can be described by two integer numbers and so by two dimensional matrix were these numbers are its indexes.
During update of matrices of probabilities Po and P1 before next time step both these indexes of are calculated by formula (1). First one scr directly for current situation and scr+ for virtual one when L[i,j] has one integer unit more.
Thus values scr and scr+ in software codes can be represented by integer values so they also can be used as indexes of two dimensional matrices pbo[Sm, Sm] and pb1[Sm, Sm] these contains pre-calculated probabilities for molecule to move for all existing combinations of scr and scr+. Formulas for calculation of probabilities to be added to the crystal, emitted from crystalline surface or stay on the same position to the next step, p+ , p- and po are presented in description of physical background of the model for numerical simulation of crystal growth.
Other method for reducing number of operations in algorithm is based on the optimization of updating procedure for matrices of probabilities to move of elements of matrix L, Po and P1. A list of all elements are in need to be updated, these includes all elements these changed position plus their neighbors, is created by algorithm at any time step. If size of the list is larger than number of all elements in active field of simulation all elements will be updated. Otherwise only elements in the list needed recalculation of probabilities are updated. This method produces most saving of calculation time for situation of to two dimensional nucleation, exactly when it is mostly important to make many time steps to achieve stable results.
The algorithm described above works close to theoretically achievable rate retaining complete integrity of underlined scientific formulas. The main acceleration compare to naive calculation with float values using exponent functions are coming because two major features: first one that it operates only with integer numbers and second that all repeated operations namely calculations of probabilities, these include exponential functions, are done in advance at preparation to simulation run with results stored in operative memory for fast reference as values of integer arrays.
The software algorithm of numerical simulation experiment for described above model also can be also summarized as sequence of following steps:
- Pre-calculation of arrays of probabilities for molecule to incorporate into crystal pb1τ or stay on its place pboτ for all thinkable combinations of the molecule's neighborhood according to formulas described in the chapter for scientific background of the method. These matrices are stored in operative memory for reference during simulation.
- For each element of active simulation field two integer matrices of normalized probabilities to move are calculated by simple conditional algorithm that give parts of molecule in direct contact with crystal body at its current position and also in virtual position as if it already moved ahead with all its neighbors retain their positions. Elements of first matrix, P1,contain values of probability for molecule to be incorporated into surface. Second matrix, Po, represents probabilities of the element not to move at all. Values of probabilities are scaled toward maximum number that can be produced by random numbers generator.
- A value of each element of matrix after current time step will be defined by comparison of generated pseudo random number with corresponding values of matrices Po and P1 to define would molecule be in, out or stay the same value. In the modification of algorithm that taking into consideration formation of hole like defects there would be options to add two or more integer units ahead when hole-type defect trapped inside crystal or when such defects is opened two or more steps back will be made.
- Depend on number of molecules at the surface these changed a position, the update of probabilities for move surface at any location affected by change will be performed before the next step. If the number of needed to update affected positions is smaller compare to number of molecules on surface only probabilities of affected molecules on the locations of change and their direct neighbors will be recalculated. Otherwise there will be recalculation of probabilities for all molecules on active field of surface.
- Steps 3-4 are repeating indefinitely long in infinite loop until user will command to stop or in automatic research mode a set criteria of completion of the numerical calculation will be met. In between time steps intermediate situations can be calculated and shown in real time for manual control.
In spite of relatively straightforwardness of scientific background of the model the software implementation demands a few states of art solutions to increase effectiveness to the level of practical applicability. The critical point is to pre-calculated and save in operative memory most of intermediate values that permits saving of processor time from repeatedly calculated time consuming procedures needed for exponent functions, multiplication and division to use instead only integer sum and subtraction operations with indexes and values of integer matrices .
In details the algorithm can be learned through step-by-step examination its specific software implementation done in C++ codes project that can be provided on the base of case by case negotiations.
Oct. 24, 2017; 11:39 EST