Deposition of epitaxial films of multicomponent compounds by magnetron sputtering, with YBa2Cu3O7-δ as an example.

by Leonid Sakharov

With the high-temperature superconductor YBa_{ACADEMY OF SCIENCES USSR

Technical Physics 38(7).

July 1993. p. 176-186

offprint (rus))

The development of microelectronics brings to the fore the problem
of high-quality films of complex chemical composition corresponding
to the phase diagram of the compounds, having special properties such as
high-temperature superconductivity, semiconducting properties,
ferromagnetism, and others. One of the promising techniques by
which it possible to unify the deposition of various materials
is magnetron sputtering.¹

This paper discusses the technological aspects of magnetron sputtering
for obtaining high-quality films of the high-temperature superconductor
YBa₂Cu₃O_{7 -δ}

The preparation of thin films of YBa₂Cu₃O_7
-δ by magnetron sputtering of stoichiometric targets has been
described in the literature. ^{1 - 8} We have obtained high-quality superconducting
films with the onset of the resistance drop (Fig. 1) at 95 K
and have obtained zero resistance at 85-89 K for oriented SrTiO₃
substrates, at 82-85 K for MgO substrates, and 75-79 K for silicon substrates
with a buffer layer of ZrO₂ by means of magnetron
sputtering using a system shown diagrammatically in Fig. 2.

The sputtered target was a ceramic disk of composition YBa₂Cu₃O_{7
-δ} of diameter 40 mm and a thickness of from 2 to 4
mm, which was attached by a silver contact to the cathode.

The total pressure of the argon -oxygen mixture with an Ar/O₂
ratio between 3 and 10 was maintained at 0.2 to 0.4 torr and
was monitored by means of a movable-electrode gas-filled tube
with an accuracy of 10%. In addition, the rate of flow of argon
directly into the discharge space was monitored, as was the supply
of oxygen at a distance of several centimeters from the substrate.
It was shown that to obtain high-quality films the rate of flow
of argon from the magnetron must exceed the order of magnitude
of 10⁴ cm/s.

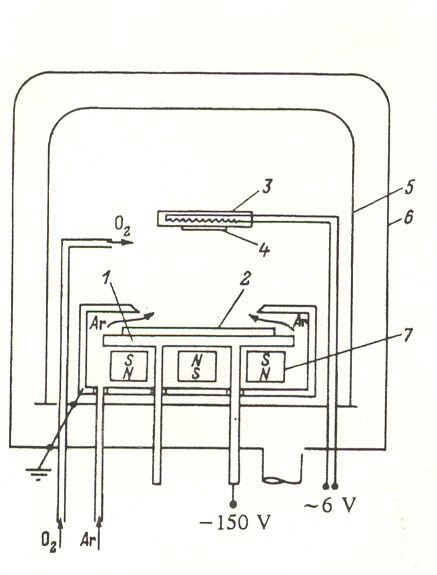
FIG. 1. Diagram of the magnetron sputtering system. 1) cathode;
2) sputtered target; 3) heating element; 4) substrate; 5) inner
cover; 6) vacuum chamber wall; 7) magnetic system

The magnetic system ensures a stable annular discharge with a
ring diameter of 25 mm and a width of 6 mm. In steady-state discharge
the discharge voltage lies between 140 and 160 V. An increase
in the discharge voltage indicates that either the resistance of the target is
increasing because of heating and the reduction of its oxygen
content below that which gives it its high conductivity, or because
of the pulverization of the anode ring, as a result of which
the voltage drop at the anode increases.

The substrates were positioned at a distance of 22 to 28 mm from
the target on a heater⁹ consisting of a high-alumina ceramic into which a platinum
or a nichrome wire was impressed at a temperature of 1200°C.
The temperature of the substrate was monitored with a Pt/Pt+
l0%Rh thermocouple attached to a control substrate, which allowed
measurement of the true substrate temperature during the deposition
with allowance for the thermal barrier between the surface of
the heater and the substrate in vacuum, which was usually found
to be in the range 200-300°C.

The temperature of the substrate surface during the deposition
was maintained in the range 650-750°C with the film deposited
at a rate of 1.5 - 5 nm/s. After admission of oxygen to a pressure
of 1 atm the sample was saturated with oxygen at a temperature
of 550°C, with subsequent cooling to 400°C at a rate of about
5 degrees per min.

Deviations from these technological parameters resulted in irreversible
degradation of the film quality. It is of interest to analyze
the technological conditions of the deposition of single phase
coatings for the purpose of creating a theoretical basis for
a systematic optimization of the apparatus configuration and the technological
conditions in formulating the problem of obtaining high-quality
films on substrates having dimensions of the order of a square
decimeter and greater.

The main advantage of magnetron sputtering systems is that the
fluxes of the evaporating atoms are in the same ratio

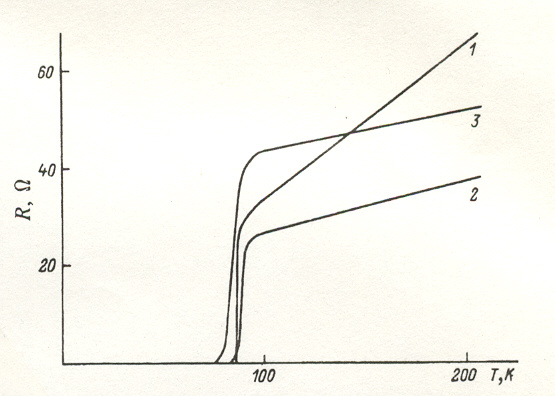
FIG. 2. Temperature dependence of the resistance of YBaa₂Cu₃O_{7
-δ} films prepared by magnetron sputtering onto a substrate
of SrTiO_j (1), MgO (2), and Si, with a protective
coating of ZrO₂ (3).

as the composition of the target. Let us consider the expression
for the flux of atoms of the itth species in the target
for a discharge that etches away the surface at a velocity V_etch.
According to Fick's law, the expression for the flux of atoms
at a distance x from the surface of the target in a system of
coordinates moving with the velocity of etching of the target is

(1)

where c_i(x) is the concentration of the ith
component of the target at a distance x from the target and D_i(x)
is the diffusion coefficient of the ith atom.

Under steady-state conditions, when the rate of sputtering V_etch
is greater than the diffusion rate of the atoms in the target
the concentration gradient of the atoms will be zero at a sufficiently
large distance from the target surface and expression (1) can
be reduced to the following expression for the fluxes of the evaporating atoms

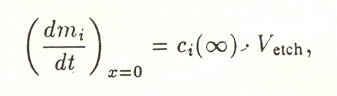
(2)

where c_i(∞) is the concentration of the ith
component sufficiently far from the target surface and is equal
to the initial concentration in the target under steady-state conditions.

Since the value of V_etch is the same for each species
of atom, it can be said that for the steady-state case the ratios
of the fluxes of the evaporating atoms correspond to the initial composition
of the target.

If the target is replaced or if the discharge current is changed
it can take several hours to reestablish a steady-state discharge
regime characterized by a steady-state distribution of the atoms
in forepart of the target surface. A suitable criterion for the establishment
of steady-state conditions is the attainment of a constant discharge
voltage. An important technological factor that permits attainment
of the steady-state regime of sputtering is good thermal contact
between the target and the water-cooled cathode, which can be
obtained by the use of silver contact paste. If the thermal contact is poor the
target is heated by the discharge and the diffusion rate then
increases exponentially and above a certain temperature can exceed
the rate of sputtering, and as a consequence it is not possible
to achieve a steady state at all.

At the time of the sputtering of the target a groove is formed
in the discharge region with a configuration that determines
the geometry of the emission of the target atoms. As the target
is continually operated the width of the planar bottom of the
groove, which permits the atoms to be emitted perpendicular to
the plane of the target, decreases in size and finally disappears
altogether, after which the cross section of the groove takes
the form of a semicircle. At this point in time the rate of transport
of atoms to the substrate falls off abruptly and the stoichiometry of the
deposited film is perturbed to the extent that a new target is
needed. The characteristic time that a target with a 6 mm groove
can be used at a current density of 2 nm/s before it must be replaced is 100 h.

The target atoms ejected by argon ion bombardment have an energy
of the order of 1 to 10 eV, which is much greater than the energy
of thermal motion, 0.02 eV. As a result of collisions of these
atoms with argon atoms the former lose energy, and when their
energy is close to the thermal energy there is a transition from
directed transport of target atoms to random transport obeying
the laws of diffusion.

Depending on the energy of an atom that reaches the substrate,
it can interact with the substrate surface in various ways, from
being incorporated into the crystal structure to being reflected
or even causing secondary sputtering of the target surface in
the case of especially high-energy particles. Let us consider the transport of
sputtered high-energy atoms from the target to the substrate.

Let us say that the atom ejected from the target has a mass M,
a radius R, and an energy E. As the result of a collision with
an atom of the scattering gas, which has a mass m and radius
r, the energy of the first atom is reduced to the value ¹⁰

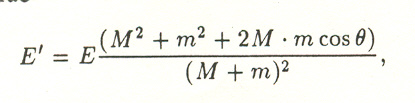
(3)

where (θ is the angle of separation in the center-of-mass
coordinate system of the colliding particles.

The angle α of deviation of the particle from its initial
direction can be calculated by the formula:

tg α = m Sin θ/(M + m*Cos θ)

(4)

An exact calculation of the scattering angles of atoms in random
collisions requires the generally unavailable knowledge

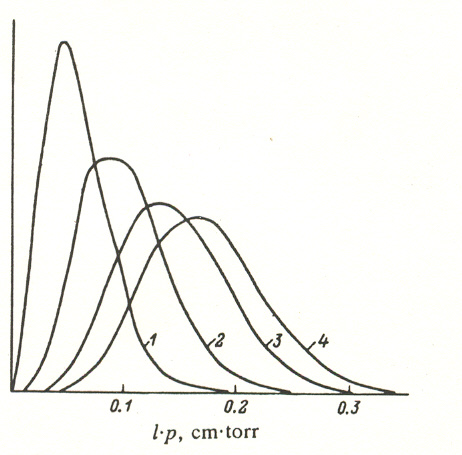
FIG. 3. Statistical curves of the reduced distance traveled by
yttrium atoms in argon until they have lost 90% (I), 99% (2).
99.9% (3), and 99.98% (4) of their initial energy.

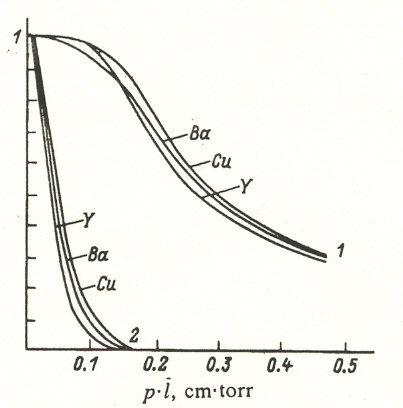
FIG. 4. Transport coefficients (I) and the fraction of atoms
that have lost no more than 90% of their initial energy (2) during
magnetron sputtering as functions of the reduced distance.

of the interaction potential of the colliding particles. Therefore
this treatment uses the simplest model for the determination
of the angle of separation for random collisions, based on the
assumption that the angle q depends
linearly on the distance between the vector of the direction
of motion of the particle and the center of mass of the scattering
atom. When the collisions are random the angle can be calculated
according to the formula

θ = (1 - √δ)*π

(5)

where d is a random quantity taking
on values uniformly distributed in the interval from 0 to 1.

The distance a particle travels between two collisions is called
the free path and can be calculated from the formula

l = ln δ/nσ = -
λ ln δ

(6)

where σ is the collision cross section equal to σ =
π(R + r)², n is the concentration of atoms in
the scattering gas, and
l is the mean free path, equal to
λ = 1/(nσ).

Figure 3 shows statistical curves of the distribution of yttrium
atoms scattered by argon atoms, plotted by means of a program
that uses the formulas given here to determine the distance travelled
by an atom before it is thermalized, when its energy is less
than a predetermined value, and to determine the amount that
the atom deviates from its initial direction of motion. Unlike
the model advanced by Danilin, ¹¹ where all the collisions result in the maximum energy
loss and the thermalization distance is determined by the formula

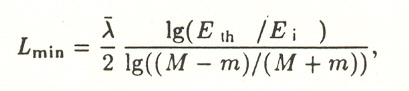
(7)

in the present case, where non-head-on collisions are also taken
into account, the average thermalization distance is 4-6 L_min,
and complete thermalization occurs at a distance of 12 - 14 L_min.

After thermalization the transport of atoms occurs by diffusion,
and in the case of the model where the target and substrate are
two infinite parallel planes the probability of deposition of
an atom on one of them is inversely proportional to the distance
of the plane from the position of thermalization.

Then the probability of transport of an atom ejected from the
target to the substrate is equal to

P_n = l_th/L

(8)

where l_th is the distance an atom travels before thermalization
and L is the spacing between the target and the substrate.

Using formulas (3)-(6) and (8) we can calculate the transport
coefficient of atoms of various species under conditions that
are characteristic of real deposition.

According to Danilin, ¹¹ bombardment by argon ions transfers to the target atoms 5 to
10% of the energy of the bombarding ions. With a discharge potential
of 150 V the energy of the sputtered atoms is estimated to be
10-20 eV, while their energy of thermal motion at 500 K, which
is the characteristic temperature in the region of the discharge,
is 0.02 eV (i.e., 10^-1 % of the initial energy).

Figure 4 shows the dependence of the transport coefficient of
atoms of Y, Ba, and Cu for these conditions, plotted as a function
of the spacing between the substrate and the target normalized
to the pressure (the reduced spacing). This figure also shows
curves that characterize the fraction of Y, Ba, and Cu atoms
that have not lost more than 10% of the initial energy ( ~ 1
eV) as a function of the reduced spacing. The characteristic
distance at which there are no particles with this high energy
coincides with the luminescent flare above the magnetron during the discharge.

Depending on the reduced target-substrate distance one can describe
the following characteristic cases of deposition of films from
a YBa₂Cu₃O_7-δ target.

In the region of existence of high-energy ions, L < 0.3 cm.torr,
the films that are deposited are superconducting, but with a
critical temperature T_c no higher than 70-75 K on SrTiO₃
substrates. According to the calculations, at this distance there
is nearly 100% transport of atoms from the target to the substrate,
but the high energy of many of the atoms that reach the substrate
either causes defects in the film or results in the reflection
of the atom and its removal without incorporation in the growing film, and
thereby the stoichiometry of the transport is disturbed.

At a reduced spacing L > 1 cm.torr all the atoms that reach the
substrate are thermalized and can be incorporated into the film,
which grows in the case of stoichiometric transport in the form
of defect-free crystals. The transport coefficients of the various
atoms can with a certain accuracy be calculated from the formula

TC_i =
L_i/L

(9)

where L_i
is the mean thermalization length of an atom of the ith
species and can be determined from data on the fluctuations in
the distribution of the thermalized Y, Ba, and Cu atoms as shown
for (E_th/E_i) = 10^-3 in Fig. 5.

With increasing target-substrate spacing the ratio of the transport
coefficients for the different atoms becomes constant. For a
stoichiometric YBa₂Cu₃O_{7 -δ}
target one should obtain under these conditions transport of
a composition that can be expressed by the formula YBa_2.4Cu_3.3O_{7
-δ} Accordingly, to obtain stoichiometric films the
process may be carried out using an adjusted-charge mixture of
composition Y_1.2Ba₂Cu_3.25O_x
for the target.

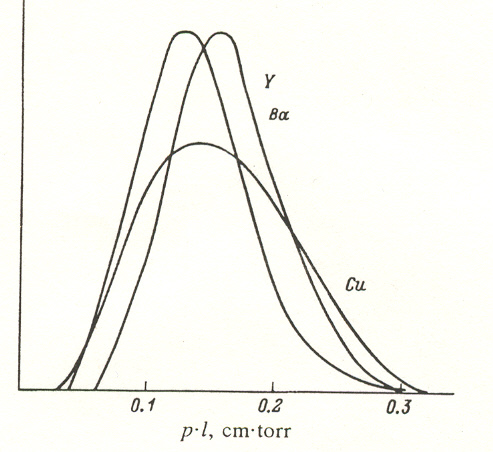
FIG. 5. Statistical curves of the reduced distances traveled
atoms of the target YBa₂Cu₃O_{7 -δ}
until they have lost 99,9% of their initial energy,

Carrying out the deposition with an adjusted charge mixture for
the target by means of dc magnetron sputtering has the disadvantage
that if the composition of the target departs from stoichiometry
its conductivity falls and the stability of the discharge can
be disrupted. Moreover, this treatment does not take into account
the unavoidable fluxes of sputtering and reaction gases, which
can have a substantial effect on the transport coefficients that are actually
observed and are characteristic of a specific design of the sputtering
system and deposition geometry.

Good results are provided by a deposition system in which the
substrate is placed parallel to the direction of motion of the
high-energy atoms.¹² In this orientation the substrate escapes bombardment by
nonthermalized atoms, and if the substrate is located at a distance.
less than L_i
the quantity TC_j turns out to be close to 100%. Since
the values of L_i
for atoms of different kinds in the present case do not differ
by more than 20%, one can expect stoichiometric transport of
the composition of the target when the substrate is located at
a distance between L_min and
L from the target.

If the velocity of gas flow in the region of diffusion transport
of thermalized atoms is comparable with the thermal velocity
of the atoms, the expression for the probability of a thermalized
atom reaching the substrate for a flow velocity V_flin
the direction from the target to the substrate takes the form

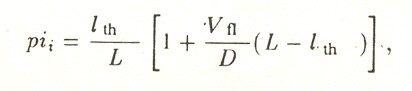
(10)

where D_i is the diffusion coefficient of the ith kind
of atom, which is approximately equal to

D_i = (1/3) *
V_iλ_i

(11)

where V_i
is the average thermal velocity of the atoms of the ith
kind in the gas, equal to

(12)

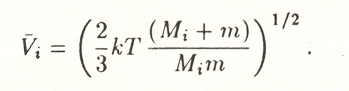
Click to request complete version of the page.

If the crystallites that are nucleated have the same orientation
their rates of growth normal to the substrate surface also turn
out to be the same and smooth films are formed with a well-formed
structure. If the substrate exerts no orienting effect or if
there exists large supercooling at reduced temperatures, where
the orienting effect of the substrate has little influence during
the nucleation, the normal component of the rate of growth of each crystallite
depends on its accidental orientation and can vary over a wide
range, and consequently the films grow with a rough surface.

REFERENCES

B. S. Danilin. Re\'iews of High-Temperature Superconductivity
[in Russian) (1991), No. 1(15). pp. 55-99.

2T. I. Selinder. G. Larsson. and U. Helmersson. Supercond. Sci.
Technol. 4. 379 (1991).

T. I. Selinder. G. Larsson. U. Hell11ersson. and S. Rudner. l.
Appl. Phys. 69.390(1991).

S. Yang. P. Wu, Z. Ji. et al.. l. Appl. Phys. 68,2308 (1990).

T. Uchiyama. M. Suzuki. and K. Takahashi. Cryog. Ellg. 25(5). 46 (1990).

H. C. Li. G. Linker, and F. Ratzel, Appl. Phys. Lett. 52, 1098 (1988).

W. Y. Lee. J. Salem. and V. Lee, Appl. Phys. LeTT. 52. 2363 (1988).

A. A. Ivanov and L. G. Sakharov. Problems in Mechanics and Mechanical
Engineering, Abstracts of a Conf. for Young Scientists, Academy
of Sciences of the USSR (1989), No.3. p. 13.

N. T. Erofeeva and L. G. Sakharov. "A heating element for vacuum
apparatus' [in Russian] . Preprint Mechanical Engineering Institutee.
Russian Academy of Sciences. Leningrad (1991), No.2 J 5-91.

Yu. V. Gomm and Yu. N. Yavlinskii, Interaction of Slow Particles
with Matter and Plasma Diagnostics (in Russian I. Moscow ( 1973).

B. S. Danilin. The Use of Low-Temperature Plasma for Deposition of Thin Films
[in Russian]. Moscow (J 989).

C. B. Eom, 1. Z. Sun, and B. M. Lairson. Physica C 171, 354 (1990).

JR. Borman and J. Nolting. Appl. Phys. Lett. 54,2148 (1991).

Y. Kubo. Y. Nakabashi, and J. Tabuchi, lpn. l. Appl. Phys. Part
2,26, L1887 (1987).

L. G. Sakharov, Processes of crystallization in anorthite-gehlenite and
gehlenite-dicalcium silicate systems' [in Russianl, Dissertation,
Leningrad (1984).

P. F. Rumyantsev and L. G. Sakharov. in: The Structure and Properties
of Silicate and Oxide Systems, Ahstracts. Bratislava (1986), pp. 89-91.

Mar. 4, 2018; 17:00 EST

Comments:}