Two-dimensional nuclei growth mechanism.
The model of two-dimensional nuclei spontaneously appeared on the surface of the crystal is the only visible explanation for layer by layer growth of the crystal that has its manifestation in smooth facets crystals. Formulas for the growth rate by two dimensional mechanism are derived from basic assumptions.The model of two-dimensional nuclei spontaneously appeared on the surface of the crystal is the only visible explanation for layer by layer growth of the crystal that has its manifestation in smooth facets crystals. Formulas for the growth rate by two dimensional mechanism are derived from basic assumptions.
The model explains observed a layer by layer growth of crystal is based on the random process of forming two dimensional nucleus. Such two dimensional nucleus is schematically displayed on the following picture:
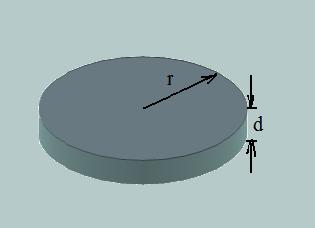
Fig. 1. Schematic view of two dimensional nucleus on the flat crystal surface.
A change of free Gibbs energy as a result of formation such disc-like island represents a formula:
| ΔG =dπr2×ΔGv + 2πrd×σ | (1), |
where r - radius of nucleus (the presumption of the disc-like shape of nucleus is based on the fact that this form provides minimum addition of surface), d - is height of nucleus and in the same time it is a size of layer, ΔGv - specific change of free energy per volume, σ- surface energy.
The dependence of change of free energy calculated by formula (1) has maximum on the curve of displaying dependence from size of nucleus as seen on the following picture:
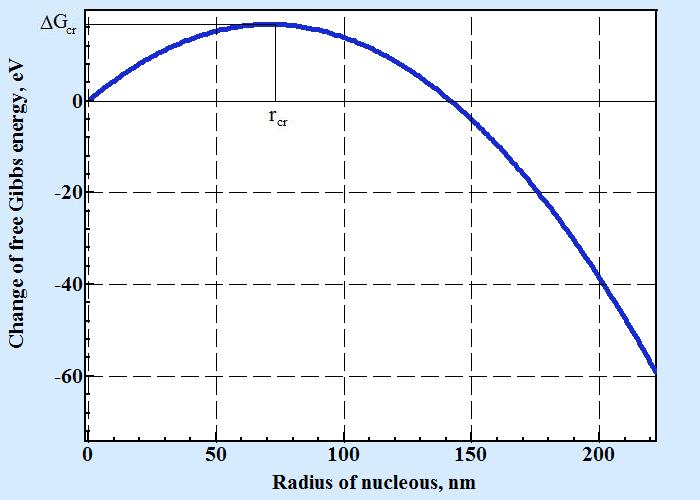
A change of free Gibbs energy shown on figure above is a function of two dimensional nucleus radius and calculated by formula 1 with following numerical parameters: cubic like molecule with size d = 0.6 nm, ΔHv = -2×10-28 J/nm3, temperature of liquidus Tl=1500o C, temperature T=1475o C, surface energy σ = 2×10-20 J/nm2.
As seen from chart for size of two dimensional nucleus less than rcr (critical radius of nucleus) a change of free energy with increasing its size is positive that thermodynamically prohibited. If molecules on crystal surface have randomly gathered into association with size above size of critical nucleus these formation is able to expanse until filling whole surface. To find size of critical nucleus one must calculate the point of maximum that is where the value of deviation of ΔG by radius must be zero:
| d ΔG | = 2dπr×ΔGv + 2πd×σ = 0 | (2) |
| d r |
resolving equation (2) toward r the analytical expression for radius of critical nucleus can be found:
| rcr = - | σ | (3) |
| ΔGv |
and change of free energy to form critical nucleus:
| ΔGcr = - | πdσ2 | (4) |
| ΔGv |
Important to point out that ΔGv ( specific change of free energy per volume) has negative sign for temperatures below of temperature of equilibrium that makes critical radius and energy of formation of critical nucleus positive.
For the model of layer by layer growth one can consider critical nuclei as constantly existing fluctuations on surface of growing crystal. Average number of molecules (positions on surface of crystal) to produce one such fluctuation can be calculated by formula:
| N = exp( | ΔGcr | ) | (5) |
| kT |
where k - Boltzmann's constant 1.38064852(79)×10-23, T - absolute (Kelvin scale) temperature.
Average radius of surface of the area on crystal filled by N molecules can be approximately defined via effective radius of molecule and presented by formula:
| Ri = N0.5× rm | (6), |
where Ri - average distance of expansion for one island grown from critical nuclei until one layer will be completely filled, rm - effective radius of one molecule.
Velocity rate of expansion of two dimensional island on surface can be taken from the thermal activated growth model where value d - heights of the layer is substitutes of the size of one molecule in plane direction: 2×rm. Taking in mind that filling of on layer equivalents to moving crystal at the distance its height the final formula for growth rate by two dimensional mechanism:
| Vn = 2×d×γo × e(-ΔGcr/2kT) ×e(-Ea in/kT) ×[1 - e(- | ΔH* ΔT | )] | (7) , |
| kTTl |
where meaning of parameters are as described for Turnbull formula in thermal activated growth model. Remarkable is that radius of molecule doesn't manifest itself into final formula. The only difference of growth rate by discussed mechanism from formula for continuous crystal growth in is a coefficient Cn:
| Vn =Cn×V | (8), |
where V - is rate of crystal growth by continues mechanism that can be defined by situation when radius of critical nucleus is less than radius of one molecule and
| Cn =2×e(-ΔGcr/2kT) | (9), |
It is important to point out that the value of correction coefficient for two dimensional nuclei growth Cn cannot be large than 1 not to contradict (10) for close to null values of energy of formation of critical nuclei. The model is not valid for radius of critical nuclei that is close to radius of molecule. Actually the consensus opinion is that area of applicability of the model of two dimensional nucleation is limited to very small supercooling where growth gem like crystals are actually observed if not universally but at least there are such phenomena reliable reported. There is an easy mathematical trick to construct normalized coefficient that will be equal to Cn for very small values and goes to 1 for big one:
| C'n = (1 - 1/Cn)-1 | (10), |
Interpretation of presented formulas should be done with great conscious. An observation of flat surface of growing crystal doesn't automatically means actualization of two dimensional nuclei mechanism. Dislocation stimulated growth and intermediate situation between two dimensional mechanism and continues growth could create flat surfaces as well. As a rule two dimensional mechanism of crystal growth should represent itself at very small supercooling. When temperature approaches Tl value of specific change of free energy ΔGv= ΔHv×(Tl- T)/Tl approaches zero and critical radius with energy of creation of critical nucleus to infinity so Cn → 0. Paradoxically at very small temperatures by absolute scale mathematically Cn → 0 as well and radius of critical nuclei rcr → σ/ΔHv so if this value is significantly large than radius of molecule one can expect that during cooling down shape of the growing crystal can be transformed from gem like crystal just below of temperature of equilibrium to dendrites with round surfaces and back to smooth flat polygon like figures at when approaching absolute zero temperature.
One of the commonly accepted criteria for determination of mechanism of growth is observed in experiment value of the power in temperature dependence of rate growth from supercooling. The empirical equation:
| V = a*exp(-E/kT)*((To- T)/T)c | (11), |
where a, E, c - coefficients are defined by approximation of experimentally obtained data for crystal growth. The value of coefficient c is supposed to be 1 for continues growth that described by Turnbull formula, for spiral dislocation growth its value should be: c=2 and for two dimensional nuclei mechanism c commonly agreed to have value about 4.5. This commonly accepted assumption for value of coefficient c in case of two dimensional mechanism is not correct. Actually as will be shown later its value is directly depend on value of surface energy and can vary from 1 to 7 and higher.
Following figure displays temperature dependences of growth rate of Al2O3 calculated by Turnbull formula with coefficient C'n as in formula (7) for series of surface energy values :
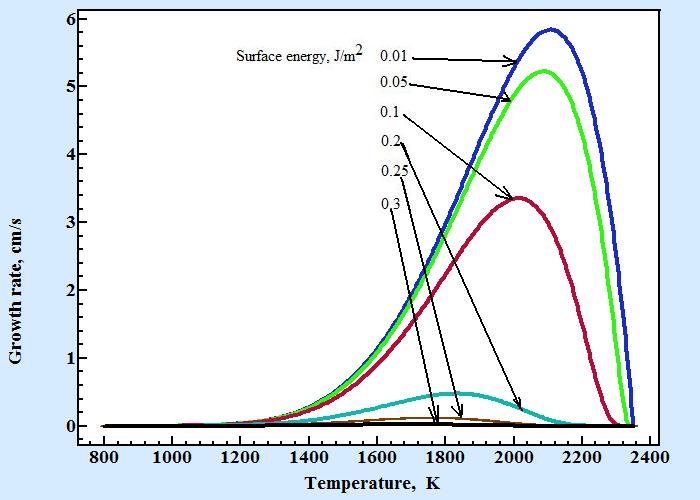
Other parameters used for calculation of growth rate are d×γ= 1×105 cm/s, Tl = 2350 K, ΔH = 2×109 J/m3, Ea = 1.45×109 J/mol and surface energy as shown at figure are taken in range from 0.01 to 0.3 J/m2. The following table contains coefficients of empirical equation 11obtained by fitting these curves:
| Surface energy, J/m2 | a, 105 cm/s | E, 105 J/mol | c, unitless |
| 0.01 | 2.9 | 1.57 | 0.84 |
| 0.05 | 3.3 | 1.58 | 0.91 |
| 0.1 | 6.8 | 1.67 | 1.29 |
| 0.2 | 329 | 2.13 | 3.46 |
| 0.25 | 4000 | 2.46 | 5.05 |
| 0.3 | 80000 | 2.86 | 6.94 |
Remarkable fact is that by varying surface energy one can mimic any value of coefficient c. The fact compromises the idea that value of power in empirical formula 11 can be used as criteria for mechanism of growth. Actually only a comprehensive investigation that includes all aspects of crystal growth from temperature dependence of shape of crystal surface and its growth rate combined with all other available information like molecular motive of crystal structure and surrounding phase, heat and mass-transport conditions must be carefully considered before making any conclusion about mechanism of the molecule incorporating into surface during crystal growth.
The most pronounces weakness of the model of two dimensional nucleation is the premise of strictly layer by layer filling of the surface. Actually only for very limited range of parameters all conditions for two dimensional nucleation could be fulfilled. Nevertheless the fact of observation of growth of perfect polygon shape crystals supports idea that such mechanism is not only theoretical excise but can actually take place in nature.
Sep. 27, 2017; 11:44 EST