Thermodynamic potential of crystal growth.
A process of phase transition of first-order such as crystallization is accompanied with heat release that reflected a difference between energy levels of crystal phase and surrounding it matter that is the 'soil' for the growing crystal. The amount of heat is equivalent to difference of enthalpies between characterized crystalline phase and in initial phase :
Qcryst =-ΔH = Hcryst - Hraw (1),
where ΔH - change of enthalpy during crystal growth, Hcryst and Hraw - enthalpies of crystal phase and initial feeding phase correspondently.
Depend on temperature crystalline area should expand itself or shrink down melting into raw phase. The criteria for the direction of the process is defined by a value of free energy potential. If it is negative a crystal will grow up otherwise if it is positive crystal will dissolve. For most practical applications the Gibbs free energy represents thermodynamic potential when temperature and pressure are constant along system. It is typical situation for material in crucible in high temperature furnace like during production of the artificial gems. Other thermodynamic potentials can be applied in special cases. The difference of Gibbs potentials in crystalline phase and feeding phase (liquid, gas or plasma) can be represented by formula:
ΔG = ΔH - ΔS*T (2),
where ΔS = Scryst - Sraw, change of entropies between crystalline and raw phases (from this point specificity sake we will talk about liquid as an initial raw phase for crystal growth), T - absolute temperature in the system (actually important that it will be temperature of the border between phases).
Entropy is a measure of disorder in the system. A crystalline phase is characterized with long-range order of atoms locations and entropy in it lower then in liquid with chaotic positions of the atoms (liquid can be characterized as material with some order in positions for near neighbor atoms and molecules). The value of changing entropy ΔS is negative the same as value of changing enthalpy ΔH for process of transformation of liquid into crystal.
The value of enthalpy changing ΔS can be defiened indirectly if heat of crystallization and a temperature of equilibrium, known also as melting point, is directly measured in experiment by calorimetry methods:
| ΔS = | ΔH | (3) , | |
| To |
where To - melting point, temperature equilibrium temperature when growth rate is effectively zero. Changing of Gibbs free energy in this case can be presented in form:
| ΔG = | ΔH*ΔT | (4) , | |
| To |
where ΔT = To - T , is often called supercooling. Note that if temperature less than equilibrium and keeping in mind that ΔH, the change of enthalpy is negative too than ΔG, change of Gibbs thermodynamic potential, is less than zero and crystal will grow up. It is slightly confusing but the mnemonic rule is that there is some most important characteristic for crystal growth namely melting point. The more temperature is deviate down from melting point the larger thermodynamic force of crystallization is.
The discussion above was limited to the case when chemical composition of noncrystalline phase is the same as for growing crystal. Like it for the case of pure water for example. In real life it is never the case as soon the are always impurity additions in any material. Formula (2) has to be amended by adding term represented a chemical potential of crystal phase in initial noncrystalline surrounding:
ΔG = ΔH - ΔS*T + k*T*ln(Ccr) (5),
where k - Boltzmann's constant (1.380 6504(24) × 10-23 J× K-1 ), Ccr - effective concentration of crystal elements in initial phase, ln() is a natural logarithm function. The expression an "effective concentration" of crystal elements demands clarification. In some sense it is quite straightforward. Let's do imaginary experiment cooling down water when some amount of of alcohol dissolved in it. The concentration, Ccr, in formula (5) can be defined as ratio between numbers of molecules of water in solution to whole number of molecules. The tricky part is that amount should be measured in molecules that is not always obviously defined number. Let say when the sample is made from two organic compounds both of them stable and do not react to each other up to the melting points represents the most clear example. In this case there is possibility to directly apply molar concentration of components in mixture to formula (5) for each of them.
But variety of situation could be very broad that brings serious complications especially in case when for some compounds like for ion salts there is no way to isolate molecule as building block of crystal structure inside its liquid solution. There is also a possibility of growth at the same time from the same initial phase more than one crystals with different compositions but the same sort of atoms. In this case there is the way to experimentally define an effective concentration for each of crystals from temperature of liquidus: Tl - that is a temperature of equilibrium for crystal with initial phase with given concentration Ccr. In this situation equilibrium (5), taking into account expression (3), can be transformed into formula:
| ln(Ccr) = | ΔH | ( | 1 | - | 1 | ) | (6) |
| k | To | Tl |
Note again that as soon ΔH has negative value liquidus value has to be less or equal than melting temperature: Tl <= To. If to make in formula (5) a substitution of changing entropy with one defined in formula (3) and value ln(Ccr) with taken from formula (6) the changing free energy of crystallization can be defined analogously like in formula (4) for crystal growth from liquid with the same chemical composition as crystal with only difference that melting temperature is replaced with liquidus temperature:
| ΔG = | ΔH* ΔT* | (7) , | |
| Tl |
where ΔT* = Tl - T .
Equation (6) has very practical sense making possible experimentally estimate melting temperature and enthalpy of crystallization even for situation when crystal of the material is not stable at melting point. A zinc oxide presents ideal example of application of indirect measurement of melting point temperature and enthalpy of crystallization on the base of data for liquidus for series of sample with different concentrations.
According to reference-books ZnO has melting point at 1975oC that is in reality temperature of its decomposition not the phase equilibrium. But the patent USA 3,043,671 "Zink oxide crystal growth method" provides the chart with data of liquidus temperatures of ZnO in eutectic solution with PbF2. Our software for data analysis was used to extract data points from the chart in the patent
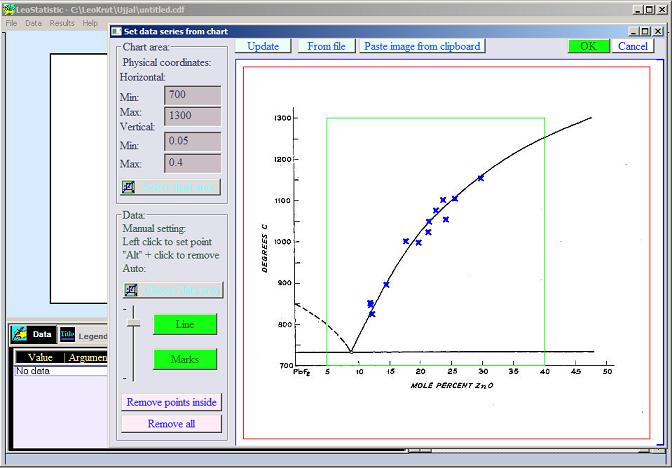
in numerical form. After converting temperature from Celsius (C) degrees into absolute Kelvin (K) scale and fitting data with equation:
ln(C) = a + b/T (8)
will be done:
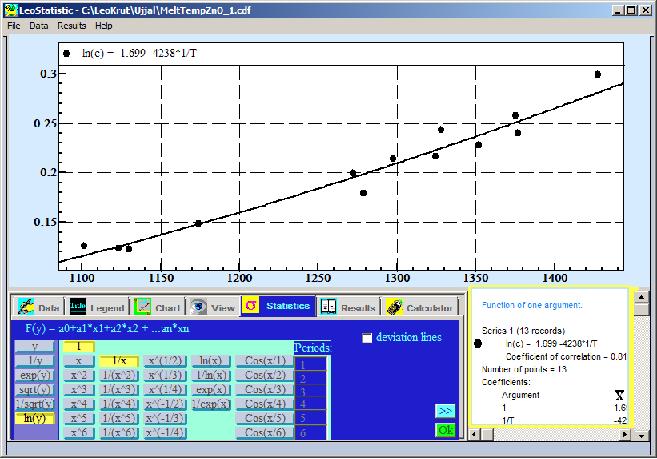
The result approximation formula can be presented with numerical coefficients: ln(C) = 1.699 -4238*1/T
Found coefficients in formula (8) are a = 1.699 and b= 4238. These values are used to calculate melting point and enthalpy of crystallization:
To = b/a = 4238/1.699 = 2494 K = 2221oC
ΔH = 1.38×10−23 JK-1 × 4.238×103 K = 5.84×10-20 J per one molecule
and molar enthalpy of crystallization:
ΔHm = ΔH × Na = 5.84×10-20 J × 6.02 ×1023 mol-1 = 35.2 kJ/mol
Sep. 26, 2017; 12:08 EST