The crystallization of glass forming melts in system anorthite-gehlenite.
ACADEMY OF SCIENCES USSR
Journal of Physics and Chemistry of Glass.
1981, v.7, N 2, p. 159-164. (
offprint)
With advance in research in glass ceramics technology, as well processing of metallurgical slag, the question of the relationship between the parameters of nonequilibrium crystallization and composition of melt it happens.
A systematic study of crystallization in the eutectic organic system of azobenzene - piperonal was first carried out in [1], where features of non-equilibrium eutectic crystallization in melts were described. Few studies have been devoted to the systematic study of crystallization in silicate eutectic systems, for example, [2-8]; which is mainly due to the large experimental difficulties of research at high temperatures.
These circumstances stimulated this work, in which a study of crystallization in the anorthite-gehlenite system (CaA12Si208 - Ca2A12SiO7) was undertaken. (Hereinafter abbreviated CAS2-C2AS) The goal was to develop a methodology for determining those crystallization parameters, knowledge of which would predict the behavior of the melt at given temperature-time effects.
To characterize the crystallization of a sample, the rate of appearance of nuclei of supercritical size and velocity their growth. The concept of the rate of growth of crystals requires an additional definition, since the crystal grows in nonequilibrium conditions The rates of displacement of the phase boundaries differ significantly in magnitude and direction at different points of the surface of the crystal. To to characterize the rate of growth of crystalline formation by a single number, we introduce the concept of a Linear Growth Rate (LGR), which is equal to the growth rate in the direction of the highest rate of growth of crystalline.
For the direct determination of LGR annealing or observation with a high-temperature microscope methods are usually used. The annealing method is used to determine LGR up to 10 -1 μm /s. The condition for its use is a much longer exposition time compared to the cooling and heating. With the help of a high-temperature microscope [9], it is possible to determine LGR up to 7.102 μm/s. In [10] the maximum values of LGR were measured. for 100 compositions of the CaO-Al2O3-SiO2 system with a melting point below 1600 ° C using these methods. However, in [10] the entire curve of the dependence of LGR from temperature was not obtained for each composition.
1. Determination of the dependence of LGR from temperature in a wide range of supercooling by means of a high-temperature microscope should be carried out by applying various methods, depending on the magnitude of the maximum value of n. from. the rate of nucleation, supercooling, the existence of metastable crystals. The following cases were identified, which required the application of an individual method:
a. The maximum value of n. c. p. does not exceed 5.101 μm/s. This is the most favorable case for measurements. The crystallized melt is gently heated to the melting temperature so that only one crystal remains in the sample, the growth rate of which is then determined after rapid cooling to the temperature of the experiment, using a lens scale with a known fission rate and a stopwatch for this.
b. The maximum LGR is more than 5.101 μm/s, and crystals are generated after external mechanical action on the surface of a molten or glass. After turning off the heater, a glass sample is obtained and, having scratched its edge, it is heated to the temperature of the experiment. Start measuring LGR crystalline formation, originated at the site of damage to the surface of the glass, is necessary after the temperature of the experiment is established, that is in about 4 s. Then for LGR 7.102 μm/s for 10 c the crystal will increase by 0.7 mm. The sample has such dimensions ( ≈ 1 mm), that a further increase in LGR will not allow us to achieve acceptable accuracy.
c. The maximum LGR more than 5.101 μm/c and there is a temperature region of bulk crystallization. In this case, each of the branches of the Tammann curve must use its own technique. For the high-temperature part, the course of the determination is similar to that indicated in a. In the region of the low-temperature branch, after rapid cooling, stop at the temperature at which such a rate of nucleation takes place, so that one or more embryos appear. Then, changing the temperature to the temperature of the experiment the LGR is measured. The region of spontaneous nucleation is not available for measurement LGR , if the crystals fall out at distances comparable with the resolving power of the microscope.
d There are compositions in which crystals of various species appear, depending on the mode of nucleation. They have, generally speaking, different n. from. p. For one temperature. l. from. p. a slower phase can only be measured if it is possible to obtain its crystal, preventing the appearance of a "fast" phase. In the region of mass nucleation of the "fast" phase, the measurement of n. c. p. "Slow" is impossible.
The determination of the type of primary precipitating crystals, as well as the degree of inhibition of growth of the secondary (driven) phase, was carried out using X-ray phase analysis. The preparation of samples for x-ray studies for many silicate compositions is complicated by the difficulty that the melt must be kept at a temperature above the melting point by 100-200°, and to use the annealing method it is necessary to be able to cool the melt in a time in which noticeable crystallization does not have time to occur. Therefore, a low-inertia high-temperature furnace (up to 2200 ° C) was created, with which it is possible to obtain samples weighing several grams for investigation on a diffractometer.
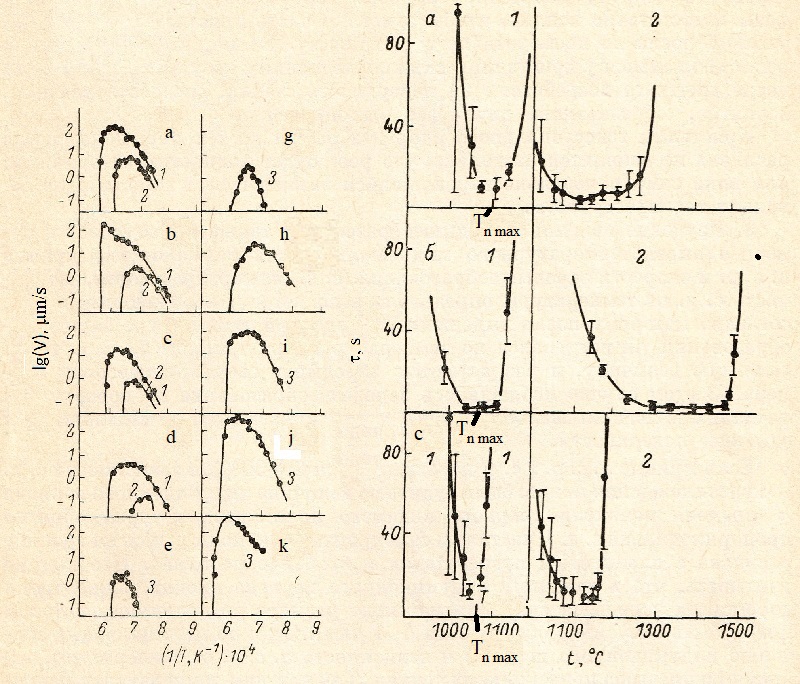
2. The Fig. 1 shows the results of measurement. LGR for ten compositions of the anorthite - gehlenite system. In four compositions in the region of 100-60% (by weight) (all compositions are given in percent by weight anorthite). Two modifications of anorthite crystals were grown. One of them, a-CAV2 (triclinic) [11], appears after external action (damage to the glass surface by a needle or local moistening). It could also spontaneously originate in glasses of compositions close to stoichiometric. Spontaneous generation also results in metastable crystals of α-anorthite hexagonal syngony [12]. in the 47-0% region, only gehlenite grows in the initial stage [13].
The general regularity of the change in the form of crystal growth was that as the supercooling increased, the degree of crystal perfection decreased. At low supercooling of the order of 20-30 °, growth of regular parallelepipeds with straight angles of gehlenite and 120 ° in hexagonal anorthite is observed, in which growth of steps on the surface was observed. With increasing supercooling in hexagonal anorthite crystals, the edges of the three diamonds constituting the hexagon are deformed in such a way that the crystal resembles a propeller. Crystals of gehlenite pass into dendrites in full accordance with the scheme described in [14].
|
|
Fig.1 Dependence of LGR from temperature in the system anorthite-gehlenite.
Melt composition: a -100, b - 85, c - 70, d - 60, e - 52.5, g
-47.5, h - 40, i - 30, j - 15, k - 0 (weight % of anorthite).
1 - triclinic anorthite, 2 -hexagonal anorthite, 3 - gehlenite.
Fig. 2 Dependence of induction period of nucleation from temperature
for Melt composition: a -100, b - 85, c - 70, d - 60.
|
The triclinic anorthite with supercooling ΔT greater than 50-100 'increases in the form of spheroids. At small ΔT ≈ 10 ° it was possible to obtain single crystals in the form of needles, but the facet like crystal was never obtained. The problem seems to be that for triclinic crystals, the layer-by-layer mechanism ensuring the formation of faceted single crystals is realized at such low supercooling that it can not be experimentally carried out. For the supercooling studied, a normal growth mechanism is realized.
Below the melting point of the eutectic, a thermodynamically stable mixture of two crystals. However, the attainment of such a mixture occurs under non-equilibrium conditions in such a way that the leading phase first grows, with the crystallization of which favorable conditions for the growth of the driven phase are created.
When the a-modification of anorthite is the leading phase, the driven phase, gehlenite, grows simultaneously with the growth of the spheroids within the leading phase, so that a eutectic crystalline formation appears, apparently according to the cooperative growth mechanism described in [1, 15].
In the part of the diagram where the leading phase is gehlenite, the growth of the driven phase of a-a-CAS2 is divided in time with the growth of gehlenite. This is probably due to the fact that although the composition of the melt is shifted towards the anorthite between the branches of the dendrites, the rate of nucleation of the driven phase is not large enough that an appreciable part of the crystalline formations grows according to the cooperative mechanism. A cooperative growth mechanism was observed in y crystalline formations with a leading phase of a-CAS2 after an external action on the glass surface, which probably contributed to the formation of two phases simultaneously.
Crystals of hexagonal anorthite grow until the composition of the melt is changed to such an extent that growth will be completely inhibited, or until spontaneously generated eutectic crystal does not fill the entire space.
3. The study of the phenomena of nucleation was also carried out using a high-temperature microscope. If the Tammann curves LGR and Nucleation Rates (NR) do not overlap, the dependence of NR from the temperature was determined by the method described in [16], according to which, after holding the sample at the nucleation temperature, it was heated to a temperature at which LGR has a noticeable value, and nuclei of supercritical size expand. In this case, nucleation on the surface of the melt was observed and the average number of crystals appearing on the unit surface was calculated.
If the curves LGR and NR. overlap (0-30%), dependence NR from supercooling could be judged from the value of the induction period τ (the time of appearance of the first visible crystal), which is inversely proportional to NR. The crystals spontaneously appeared on the boundary of the melt with a platinum heater and in the volume of the melt. It should be taken into account that the induction period also includes the time for the growth of a supercritical nucleus to a value that can be visually detected (≈ 1 μm). Judging by the minimum value of the induction period and the dependence of n. from. p. from the temperature, this time did not exceed several seconds. Since at the temperatures of the maximum nucleation after the appearance of the first crystals, the melt completely crystallizes in a few seconds, it was impossible to reliably distinguish the contribution of the nonstationary nucleation stage.
An analysis of the statistical spread τ for the same temperature showed that with an average value of τ ≈ 2 - 5 s, the standard deviation ( Δτ = (∑ ( τ - τ)/ n)2 ) approaches the instrument error ≈1 c, and with τ increase the dispersion Δτ is approximately equal to the mean value τ. This indicates that, according to [17], the value of τ can be considered inversely proportional to the nucleation rate 1/I.
In Fig. 2 shows the temperature dependence of t i for compositions in the 0-30% range. The values are obtained after 6-10 measurements. In Fig. 2 are also gives standard deviations, Δτ.
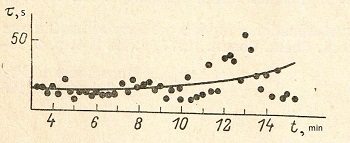
The rate of homogeneous nucleation is greatly influenced by the temperature heating time. In Fig. 3 depicts the dependence on NR of melt heating time at a temperature of 1650 ° C. It can be seen that the average value of the induction period τi and its variance for small times of heating grow relatively little as heating time increases. Since some point, τ increases nonlinearly, reaching after 1 h for a temperature of 1650 ° and the same after half an hour for 1700 ° to such an extent that it can no longer be measured due to the complete crystallization of the sample from the edges.
Thus, one can not speak NR of melt at a given temperature, distracting from the history of its receipt. Therefore, in order to characterize the process of nucleation, instead of the specific values of the velocity, it is better to use the temperature value of maximum NR, Tn max, the value of which depends little on the melting mode. At the same time, for technology needs, Tn max is often quite sufficient to select a rational heat treatment regime.
|

|
| Fig.3 Dependence of induction period of nucleation from time of the melt exposition. Points - individual measurements, line is moving average. | Fig.4 Phase diagram the system anorthite-gehlenite and values of temperatures of maximum rate of nucleation. Liquidus curves: a - triclinic anorthite, hexagonal anorthite, c - gehlenite. Tn max for: 1- gehlenite, 2 -hexagonal anorthite. |
In Fig. 4 shows the dependence of Tn max from melt composition. For compositions in interval 0 - 30% Tn max was determined from data presented on Fig. 2; for compositions in interval 30 - 100% on the Pt surface melt - air with method of preliminary exposition [16]. It is noticeable that Fig. 2 and 4 do not show Tn max for surface Pt-melt, because influence of specific microrelief of Pt heater and can significantly vary from sample to sample.
CONCLUSIONS. A technique is described for determining the linear growth rates of crystals and the temperature of the maximum nucleation rate in complex silicate melts using a high-temperature microscope.
The dependence of NR on the temperature and composition of the melt for crystals of gehlenite and two forms of anorthite crystals in the pseudo-binary anorthite gehlenite system were measured.
The dependence of the temperature of the maximum rate of nucleation on the composition of the melt is determined.
The measurement of the crystal growth morphology with increasing supercooling is interpreted from the point of view of the transition from the layer-by-layer growth mechanism to the normal growth mechanism.
References
1. A. Bochvar, Investigation of the mechanism and kinetics of crystallization of eutectic-type alloys. m. l. , 1936. 82 p.
2. Zschimmer E. The velocity of crystallization in soda-lime-silica glasses. J. Soc. Glass. Technol. , 1929, v. 13, No. 49, p. 76-84.
3. Kirkpatrick I. R. Kinetic of crystal growth in the system CaMgSi206 CaAl2Si06. Amer. J. Sci., 1974, v. 274, No. 3, p. 215-242.
4. Rumyantsev PF, Siroko IP, Degen MG Effect of Cr203 on the crystallization of Glasses of the gehlenite -volastonite system. l., 1.970. 7 c. (manuscript deposited in VINITI, N 2577-71-Dep.).
5. Rumyantsev P. F, Siroko I. P Kinetics of the Crystallization of Gehlenite in Glass. l. , 1970. 10 s. (manuscript of deposited in VINITI, 2576-71-Dep.).
6. Ziemba. B., Ziemba W., Hanczak K. Zaleznose podatnoschi do krystalizayi od skxadu chemicznego szkiex z ukladu Si02 -Ā1203 -Ņā0- Mg0 -Nā20. Szklo i Ceramika, 1976, V. 27, No. 3, p. 57-59.
7. Kurchinin I. L., Ivanova L. V., Dorofeeva I.M. Crystal glass of slag glasses. Izv. AN USSR. Inorgan. mater. , 1968, Vol. 4, 2, p. 269-273.
8. Strad Z., Douglas R. W. Nucleation and crystallization in the soda-lime-silica system. Phys. Chem. Glasses, 1973, v. 14, No. 2, p. 33 36.
9. Leonov A .I., Rumyantsev P. F High-temperature microscope. M., 1964. 3 p.
10. Kumm K.-A., Scholze N. Die Kristallisationgeschwindigkeit von schlackenschnlelzen in system Ca0 -A1203 -Si02. Tonind-Ztg., 1969, Bd 93, N 9, 8, s. 332-337; N 10, s. 360-363.
11. H. Borg I. Y., smith D. K. Calculated powder patterns. I. Five plagioclases. Amer. Mineral., 1968, v. 53, No. 9, p. 1709 17 23.
12. Davis G. L., Tuttle OR Two new crystalline phases of anorthite composition. Amer. J. Sci., Bowen vol., Pt. 1, 1.952, p. 107 114.
13. Ervin I. .F. , Osborn, E. F. X-ray data on synthetic melilites. Amer. Mineral,, 1938, v. 34, No. 9, 10, p. 717-722.
14 Sapatovkin D. D .. Dendrite crystallization. M. , 1957. 96 c.
15. Mazur VN, Osetrov S. A., Taran Yu. N. Diffusion mechanism of cooperative eutectic crystallization. Izv. AN USSR. Metals, 1976, Vol. 6, No. 2, p. 126 -128.
16. Filipovich V. N, Kalinina A.M About regularities of nucleation of the crystalline phase in glasses. In. : Problems of silicate chemistry. L., 1914, p. 219-232
17. Horsak J., Pacak R., Slarna J. Ein 8tochastiches Modell der Kristallisation au unter-kihlten Fltissigkeiten. Coil. Czech. Chem. Comm., 1.977, v. 42, No. 4, p. 1100-1107.
Institute of Silicate Chemistry them. I.V. Grebenschikov AN of the USSR Leningrad moved to Redanzpi February 6, 1980 Received February 6, 1980;
Feb. 22, 2018; 15:38 EST