Dislocation induced crystal growth
The dislocation induced mechanism of crystal growth is based on premise that imperfections on the flat surface of the crystal can play the role of two dimensional nucleus bypassing necessity of their spontaneous appearance to produce layer by layer growth. For the special case of spiral dislocation a derivation of the analytical formula for the growth rate with square dependence from supercooling is presented.
There is apparent contradiction between observation of crystals these are growing in form of perfect geometrical figures with flat surfaces and outcome of formulas for two dimensional nuclei growth mechanism these predict that rate of crystal surface by layer by layer progression should be too slow to be noticed. The theoretical growth rate predicts too small values for perfect shape crystals to be observed in nature at all. In the same time on the surface of the crystals were observed spiral like formations. That lead to development of the separate standing theory of crystal growth named spiral dislocation model.
This model bypasses the necessity of random formation of two dimensional nuclei on the flat, completely filled, surface of crystal by presuming a permanent presence of dislocations on it. Dislocations are local deviations from perfect crystal structure on the atomic level. Sources of dislocations could be isomorphic substitution of one atom by other one with close chemical properties; holes inside crystal due not complete filling one layer that will be covered by other. Some positions could be left not filled and trapped inside. Taking aside for now the source of dislocation do postulate their presence as axiom.
A dislocation on the surface could be considered as effective shortcut around necessity of critical nucleus formation on the flat surface. Analytical solution of such situation for general case of random distribution of dislocations with different acceleration effects on the rate of formation of overcritical nuclei on the surface of growing crystal is if not impossible but obviously useless for now and due to lack of direct measurement can not be compared with experiment. After invention of force microscopy that problem is maybe will be pursued sometimes later. For now the only thing that can be done legitimately for such general problem is just add correction coefficient to the theoretical value for energy of formation of critical nuclei.
There is a special case of so named spiral (screw) dislocation growth. If inside crystal structure there is partial shift of layers in direction perpendicular to the surface like it is shown in the picture:
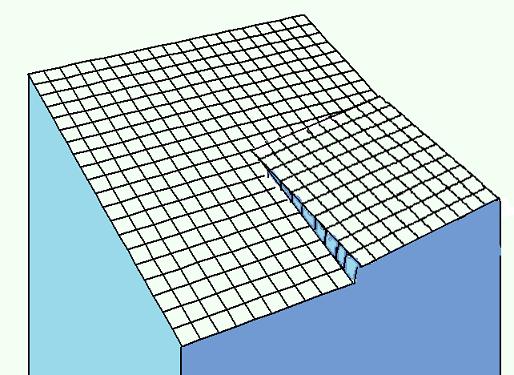
The ledge on surface can internally reproduce itself creating preferable area for surface growth. Further expansion can take a form of spiral like it is shown on the photo:

One can find analogy with pulsar sending wave by wave these are covering surface of crystal one layer of molecules by another.
The growth rate of surface with such spiral defect is defined by rate of progressing of its tip. Obviously that average curvature on the tip must be larger than radius of critical nucleus otherwise tip would shrink instead of growing. The rate of vertical growth of the tip can be described by formula:
| Vtip = (Sstep/Stip) Vcont | (1), |
where Vcont - the rate of continuous growth of rough surface where there are no preferable molecule position for incorporating of molecules into the crystal or emitting from it. The formula for rate for continuous growth defined by Turnbull formula;
Sstep and Stip are areas around layer step with one molecule width and whole area around tip as shown at following figure:
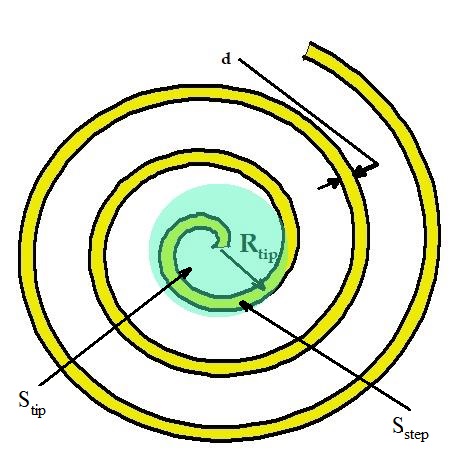
Sstepis an area situated just in contact with the step near tip of the spiral with width equal to size of one molecule and Stip is whole area around tip. Only molecule positions inside Sstep area are available for direct incorporation and emitting molecules with the same as from rough surface. If Rtip is average curvature of the tip that is approximate equal to radius of critical nucleus following equations are valid::
| Sstep = 2πd Rtip | (2), |
| Stip = πRtip2 | (3), |
where d is effective size of the molecule in parallel to the surface directions. By substituting Sstep and Stip in formula (1) from values in formulas (2) and (3) growth rate formula for spiral mechanism takes a form:
| Vtip = 2(d/Rstep)*Vstep | (4), |
where Vstep is the growth rate of the step around the tip that can
be presented by formulas for continues growth with correction for curvature of
thermodynamical potential of growth like it shown in following formula:
| Vstep =d γo*exp(-Ea in/kT)*[1 - exp( - | ΔH*ΔT | (1 - Rcr/Rtip))] | (5), |
| kTTl |
where meaning of parameters are the same as in article: thermal activation model
For small supercooling formula 5 can be simplified taking into account that (1 - exp(-x)) → x when x → 0 approaches to zero:
| Vstep =Vflat*(1-Rcr/Rtip) | (6), |
where Vflat = Vcont growth rate for flat step when curvature of the step on surface is approaching to infinity. Here is an point of possible confusion. Infinite curvature here is presumes for infinite rough surface. That looks like internal contradiction statement until you image analogy the sand paper can be bend. It would have some curvature and be rough in the same time.
Finally growth rate of spiral tip would have the equation form as:
| Vtip = 2(d/Rtip)*(1-Rcr/Rtip)* Vcont | (7), |
One can assume that curvature of the tip would be such to produce maximum possible growth of expansion. Equation 7 permits analytical finding expression for Rtip that produces maximum growth rate:
| Rspiral = 2*Rcr | (8), |
and
| Vspiral = 0.5*(d/Rcr)*Vcont = 0.5*ΔH/(d*σ)*(ΔT/Tl)*Vcont | (9), |
Obviously the equation (9) has limitations for large supercooling when radius of critical nuclei is smaller or just comparable to size of molecule. For such circumstances a continues growth rate should be expected.
It is worst to note that analytical solution can be found also for equation (5) but with caviar that final formulas are too massive and don't presented any qualifiedly novel conclusions compare with formula (9) information to be present here.
Taking into account that Vcont has linear function of supercooling and coefficient presented influence of spiral mechanism of growth is linear function of supercooling as well hence the growth rate by spiral mechanism should be a square function of supercooling.
Sep. 28, 2017; 10:06 EST